
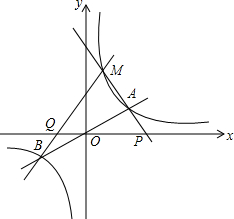
 如图,已知双曲线y=$\frac{{k}_{1}+3}{x}$(k1为常数)与直线y=k2x(k2为常数)相交于A,B两点,双曲线在第一象限内部分有一点M(点M在A的左侧)在双曲线y=$\frac{{k}_{1}+3}{x}$上,设直线MA,MB分别与x轴分别交于P,Q两点.若MA=m•AP,MB=n•QB,则n-m的值是2.
如图,已知双曲线y=$\frac{{k}_{1}+3}{x}$(k1为常数)与直线y=k2x(k2为常数)相交于A,B两点,双曲线在第一象限内部分有一点M(点M在A的左侧)在双曲线y=$\frac{{k}_{1}+3}{x}$上,设直线MA,MB分别与x轴分别交于P,Q两点.若MA=m•AP,MB=n•QB,则n-m的值是2. 分析 作MH⊥y轴,AN⊥y轴,BI⊥y轴分别于点H、N、I,则MH∥AN∥BI,ON=OI,根据平行线分线段成比例定理即可求解.
解答 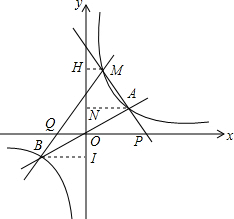 解:作MH⊥y轴,AN⊥y轴,BI⊥y轴分别于点H、N、I,则MH∥AN∥BI.
解:作MH⊥y轴,AN⊥y轴,BI⊥y轴分别于点H、N、I,则MH∥AN∥BI.
∵反比例函数是中心对称图形,
∴ON=OI.
∵MH∥AN∥BI,MA=m•AP,MB=n•QB
∴m=$\frac{MA}{AP}$=$\frac{HN}{ON}$,n=$\frac{MB}{BQ}$=$\frac{HI}{OI}$=$\frac{HN+ON+OI}{OI}$,
又∵ON=OI,
∴n=$\frac{HN+2ON}{ON}$=$\frac{HN}{ON}$+2=m+2,
∴n-m=2.
故答案是:2.
点评 本题考查了平行线分线段成比例定理和一次函数与反比例函数的应用,关键是根据平行线分线段成比例定理得出比例式,题目比较好,但有一定的难度.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:解答题
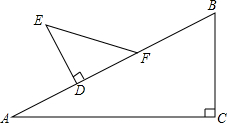 如图△ABC中,∠C=90°,∠A=30°,BC=5cm;△DEF中∠D=90°,∠E=45°,DE=3cm.现将△DEF的直角边DF与△ABC的斜边AB重合在一起,并将△DEF沿AB方向移动(如图).在移动过程中,D、F两点始终在AB边上(移动开始时点D与点A重合,一直移动至点F与点B重合为止).
如图△ABC中,∠C=90°,∠A=30°,BC=5cm;△DEF中∠D=90°,∠E=45°,DE=3cm.现将△DEF的直角边DF与△ABC的斜边AB重合在一起,并将△DEF沿AB方向移动(如图).在移动过程中,D、F两点始终在AB边上(移动开始时点D与点A重合,一直移动至点F与点B重合为止).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知抛物线经过A(-1,)、B(3,0),C(0,3),点D为抛物线的顶点.
已知抛物线经过A(-1,)、B(3,0),C(0,3),点D为抛物线的顶点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 尼泊尔地震牵动着全中国人民的心,中国红十字基金会开展了“一方有难,八方支援”的赈灾活动.5月15日,中国红十字基金会联手北京成龙慈善基金会等共同出资400万元人民币,采购5000只“赈济家庭箱”(“赈济家庭箱”包括当地受灾群众急需的毛毯、防潮垫、睡袋、雨衣、服装、餐具、个人护理用品等),作为首批物资援助尼泊尔地震灾区.该基金会计划到第三批援助物资为止共采购18200只“赈济家庭箱”.
尼泊尔地震牵动着全中国人民的心,中国红十字基金会开展了“一方有难,八方支援”的赈灾活动.5月15日,中国红十字基金会联手北京成龙慈善基金会等共同出资400万元人民币,采购5000只“赈济家庭箱”(“赈济家庭箱”包括当地受灾群众急需的毛毯、防潮垫、睡袋、雨衣、服装、餐具、个人护理用品等),作为首批物资援助尼泊尔地震灾区.该基金会计划到第三批援助物资为止共采购18200只“赈济家庭箱”.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com