
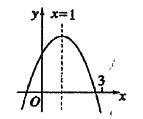
【题目】二次函数![]() 图象如图,下列结论中正确的是( )
图象如图,下列结论中正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
由抛物线的开口方向和对称轴的位置可确定a,b的符号,由抛物线与y轴的交点可确定c的符号,由对称轴x=1可确定2a与b的关系,由特殊点的位置可确定D的正误,由二次函数的增减性可确定⑤的正误..
解:∵抛物线开口向下,
∴a<0,
∵-![]() >0,
>0,
∴b>0,
∵抛物线与y轴的交点在x轴上方,
∴c>0,
∴abc<0,所以A错误;
∵抛物线对称轴为直线x=-![]() =1,
=1,
∴b=-2a>0,即2a+b=0,所以B错误,C正确;
∵抛物线与x轴的一个交点在(3,0)的左侧,而对称轴为直线x=1,
∴抛物线与x轴的另一个交点在(-1,0)的右侧,
∴当x=-1时,y<0,
∴a-b+c<0,所以D错误;
故选:C.


科目:初中数学 来源: 题型:
【题目】如图,BE是⊙O的直径,半径OA⊥弦BC,垂足为D,连接AE、EC.

(1)若∠AEC=25°,求∠AOB的度数;
(2)若∠A=∠B,EC=4,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系![]() 中的点
中的点![]() 和
和![]() ,给出如下定义:连接
,给出如下定义:连接![]() 交
交![]() 于点
于点![]() ,若点
,若点![]() 关于点
关于点![]() 的对称点
的对称点![]() 在
在![]() 的内部,则称点
的内部,则称点![]() 是
是![]() 的外称点.
的外称点.
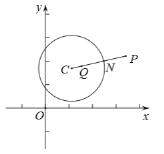
(1)当![]() 的半径为
的半径为![]() 时,
时,
①在点![]() 中,
中,![]() 的外称点是 ;
的外称点是 ;
②若点![]() 为
为![]() 的外称点,且线段
的外称点,且线段![]() 交
交![]() 于点
于点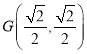 ,求
,求![]() 的取值范围;
的取值范围;
(2)直线![]() 过点
过点![]() , 与
, 与![]() 轴交于点
轴交于点![]() .
. ![]() 的圆心为
的圆心为![]() , 半径为
, 半径为![]() 若线段
若线段![]() 上的所有点都是
上的所有点都是![]() 的外称点,请直接写出
的外称点,请直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列一组方程:①![]() ,②
,②![]() ,③
,③![]() ,…小明通过观察,发现了其中蕴含的规律,并顺利地求出了前三个方程的解第①个方程的解为
,…小明通过观察,发现了其中蕴含的规律,并顺利地求出了前三个方程的解第①个方程的解为![]() ;第②个方程的解为
;第②个方程的解为![]() ;第③个方程的解为
;第③个方程的解为![]() .若n为正整数,且关于x的方程
.若n为正整数,且关于x的方程![]() 的一个解是
的一个解是![]() ,则n的值等于____________.
,则n的值等于____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】锐角△ABC中,BC=6,![]() ,两动点M,N分别在边AB,AC上滑动,且MN∥BC,以MN为边向下作正方形MPQN,设其边长为x,正方形MPQN与△ABC公共部分的面积为y(y>0).
,两动点M,N分别在边AB,AC上滑动,且MN∥BC,以MN为边向下作正方形MPQN,设其边长为x,正方形MPQN与△ABC公共部分的面积为y(y>0).
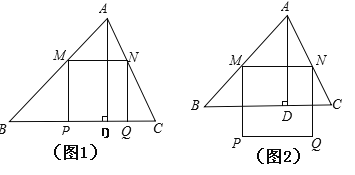
(1)求△ABC中边BC上高AD;
(2)当x为何值时,PQ恰好落在边BC上(如图1);
(3)当PQ在△ABC外部时(如图2),求y关于x的函数关系式(注明x的取值范围),并求出x为何值时y最大,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山西汾酒,又称“杏花村酒”.酿造汾酒是选用晋中平原的“一把抓高粱”为原料.汾阳县某村民合作社2016年种植“一把抓高粱”100亩,2018年该合作社扩大了“一把抓高梁”的种植面积,共种植144亩.
(1)求该合作社这两年种植“一把抓高梁”亩数的平均增长率;
(2)某粮店销售“一把抓高粱”售价为13元/斤,每天可售出30斤,每斤的盈利是1.5元.为了减少库存,粮店决定搞促销活动.在销售中发现:售价每降价0.1元,则可多售出2斤.若该粮店某天销售“一把抓高梁”的盈利为40元,则该店当天销售单价降低了多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的三个顶点A(1,2)、B(2,2)、C(2,1).以原点O为位似中心,将△ABC扩大得到△A1B1C1,且△ABC 与△A1B1C1的位似比为1 :3.则下列结论错误的是 ( )
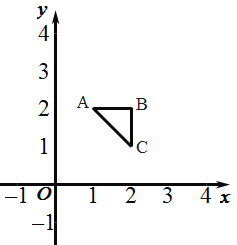
A.△ABC∽△A1B1C1B.△A1B1C1的周长为6+![]()
C.△A1B1C1的面积为3D.点B1的坐标可能是(6,6)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究:
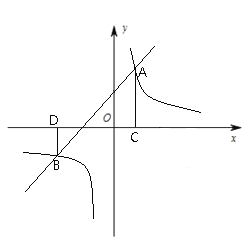
如图所示,在平面直角坐标系中,直线![]() 与反比例函数
与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点,过点
两点,过点![]() 作
作![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() .
.
(1)求![]() ,
,![]() 的值及反比例函数的函数表达式;
的值及反比例函数的函数表达式;
(2)若点![]() 在线段
在线段![]() 上,且
上,且![]() ,请求出此时点
,请求出此时点![]() 的坐标;
的坐标;
(3)小颖在探索中发现:在![]() 轴正半轴上存在点
轴正半轴上存在点![]() ,使得
,使得![]() 是以
是以![]() 为顶角的等腰三角形.请你直接写出点
为顶角的等腰三角形.请你直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com