
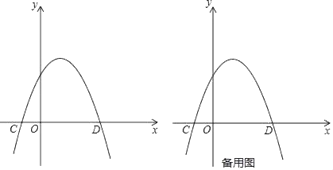
【题目】在平面直角坐标系![]() 中,规定:抛物线
中,规定:抛物线![]() 的伴随直线为
的伴随直线为![]() .例如:抛物线
.例如:抛物线![]() 的伴随直线为
的伴随直线为![]() ,即
,即![]() .
.
(1)在上面规定下,抛物线![]() 的顶点为 .伴随直线为 ;抛物线
的顶点为 .伴随直线为 ;抛物线![]() 与其伴随直线的交点坐标为 和 ;
与其伴随直线的交点坐标为 和 ;
(2)如图,顶点在第一象限的抛物线![]() 与其伴随直线相交于点
与其伴随直线相交于点![]() (点
(点![]() 在点
在点![]() 的右侧)与
的右侧)与![]() 轴交于点
轴交于点![]()
①若![]() 求
求![]() 的值;
的值;
②如果点![]() 是直线
是直线![]() 上方抛物线的一个动点,
上方抛物线的一个动点,![]() 的面积记为
的面积记为![]() ,当
,当![]() 取得最大值
取得最大值![]() 时,求
时,求![]() 的值.
的值.
【答案】(1)(﹣1,﹣4),y=x﹣3,(0,﹣3),(﹣1,﹣4);(2)①m的值为![]() ;②m=-2.
;②m=-2.
【解析】
(1)根据题干中的定义即可找出其伴随直线为y=(x+1)﹣4,即y=x﹣3,再联立抛物线求解即可
(2)①先与其伴随直线联立求得交点![]() ,再求出抛物线与x轴的交点C,D,根据∠CAB=90°由勾股定理求出m;
,再求出抛物线与x轴的交点C,D,根据∠CAB=90°由勾股定理求出m;
②设直线BC的解析式为y=kx+b.将B(2,-3m),C(-1,0)代入求出y=-mx-m.过P作x轴的垂线交BC于点Q,将三角形面积用含m的表达式表示出来即可
(1)由伴随直线的定义可得其伴随直线为y=(x+1)﹣4,即y=x﹣3,
联立抛物线与伴随直线的解析式可得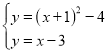 ,解得
,解得![]() 或
或![]() ,∴其交点坐标为(0,﹣3)和(﹣1,﹣4).
,∴其交点坐标为(0,﹣3)和(﹣1,﹣4).
故答案为:(﹣1,﹣4);y=x﹣3;(0,﹣3);(﹣1,﹣4);
(2)①∵抛物线解析式为y=m(x-1)2-4m,∴其伴随直线为y=m(x-1)-4m,即y=mx-5m.
联立抛物线与伴随直线的解析式可得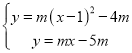 解得
解得![]() 或
或![]() ,∴A(1,-4m),B(2,-3m).
,∴A(1,-4m),B(2,-3m).
在y=m(x-1)2-4m中,
令y=0可得x=-1或x=3,∴C(-1,0),D(3,0),∴AC2=4+16m2,AB2=1+m2,BC2=9+9m2.
∵∠CAB=90°,∴AC2+AB2=BC2,即4+16m2+1+m2=9+9m2,解得:m=![]() (抛物线开口向下,舍去)或m=-
(抛物线开口向下,舍去)或m=-![]() ,∴当∠CAB=90°时,m的值为-
,∴当∠CAB=90°时,m的值为-![]() .
.
②设直线BC的解析式为y=kx+b.
∵B(2,-3m),C(-1,0),∴![]() ,解得
,解得![]() ,∴直线BC的解析式为y=-mx-m.
,∴直线BC的解析式为y=-mx-m.
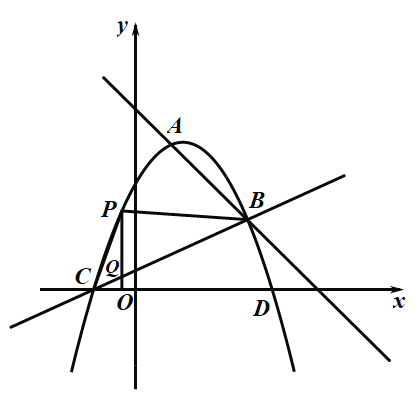
过P作x轴的垂线交BC于点Q.
∵点P的横坐标为x,∴P(x,m(x-1)2-4m),Q(x,-mx-m).
∵P是直线BC上方抛物线上的一个动点,∴PQ=m(x-1)2-4m+mx+m=m(x2-x-2)=m[(x-![]() )2-
)2-![]() ],∴S△PBC=
],∴S△PBC=![]() ×[2-(-1)]PQ=
×[2-(-1)]PQ=![]() m(x-
m(x-![]() )2-
)2-![]() m,∴当x=
m,∴当x=![]() 时,△PBC的面积有最大值-
时,△PBC的面积有最大值-![]() m,∴S取最大
m,∴S取最大![]() 时,即-
时,即-![]() m=
m=![]() ,解得:m=-2.
,解得:m=-2.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】疫情期间,甲厂欲购买某种无纺布生产口罩,A、B两家无纺布公司各自给出了该种无纺布的销售方案.
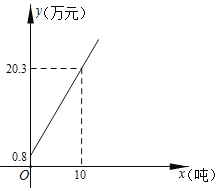
A公司方案:无纺布的价格y(万元)与其重量x(吨)是如图所示的函数关系;
B公司方案:无纺布不超过30吨时,每吨收费2万元;超过30吨时,超过的部分每吨收费1.9万元.
(1)求如图所示的y与x的函数解析式;(不要求写出定义域)
(2)如果甲厂所需购买的无纺布是40吨,试通过计算说明选择哪家公司费用较少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家创新指数是反映一个国家科学技术和创新竞争力的综合指数.对国家创新指数得分排名前40的国家的有关数据进行收集、整理、描述和分析.下面给出了部分信息:
a.国家创新指数得分的频数分布直方图(数据分成7组:
30≤x<40,40≤x<50,50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100);
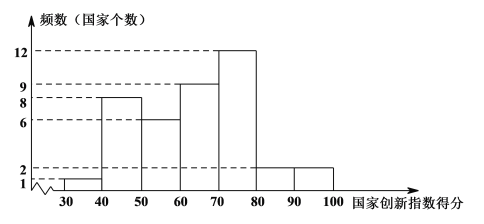
b.国家创新指数得分在60≤x<70这一组的是:61.7 62.4 63.6 65.9 66.4 68.5 69.1 69.3 69.5
c.40个国家的人均国内生产总值和国家创新指数得分情况统计图:
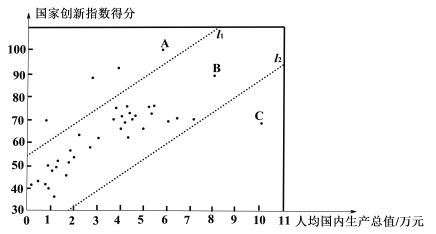
d.中国的国家创新指数得分为69.5.
(以上数据来源于《国家创新指数报告(2018)》)
根据以上信息,回答下列问题:
(1)中国的国家创新指数得分排名世界第______;
(2)在40个国家的人均国内生产总值和国家创新指数得分情况统计图中,包括中国在内的少数几个国家所对应的点位于虚线![]() 的上方.请在图中用“
的上方.请在图中用“![]() ”圈出代表中国的点;
”圈出代表中国的点;
(3)在国家创新指数得分比中国高的国家中,人均国内生产总值的最小值约为______万美元;(结果保留一位小数)
(4)下列推断合理的是______.
①相比于点A,B所代表的国家,中国的国家创新指数得分还有一定差距,中国提出“加快建设创新型国家”的战略任务,进一步提高国家综合创新能力;
②相比于点B,C所代表的国家,中国的人均国内生产总值还有一定差距,中国提出“决胜全面建成小康社会”的奋斗目标,进一步提高人均国内生产总值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学艺术节期间,学校向学生征集书画作品,杨老师从全校30个班中随机抽取了4个班(用A,B,C,D表示),对征集到的作品的数量进行了分析统计,制作了两幅不完整的统计图.

请根据以上信息,回答下列问题:
(1)杨老师采用的调查方式是 (填“普查”或“抽样调查”);
(2)请你将条形统计图补充完整,并估计全校共征集多少件作品?
(3)如果全校征集的作品中有5件获得一等奖,其中有3名作者是男生,2名作者是女生,现要在获得一等奖的作者中选取两人参加表彰座谈会,请你用列表或树状图的方法,求恰好选取的两名学生性别相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
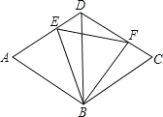
【题目】如图,边长为2的菱形ABCD中,BD=2,E、F分别是AD,CD上的动点(包含端点),且AE+CF=2,则线段EF长的最小值是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D、E、F分别是边AB、AC、BC的中点,要判定四边形DBFE是菱形,下列所添加条件不正确的是( )

A. AB=AC B. AB=BC C. BE平分∠ABC D. EF=CF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应“书香学校,书香班级”的建设号召,平顶山市某中学积极行动,学校图书角的新书、好书不断增加.下面是随机抽查该校若干名同学捐书情况统计图:
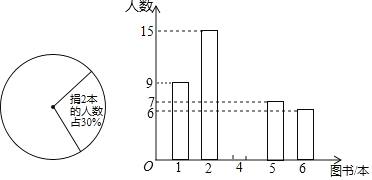
请根据下列统计图中的信息,解答下列问题:
(1)此次随机调查同学所捐图书数的中位数是 ,众数是 ;
(2)在扇形统计图中,捐2本书的人数所占的扇形圆心角是多少度?
(3)若该校有在校生1600名学生,估计该校捐4本书的学生约有多少名?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com