
如图,二次函数 的图象与一次函数
的图象与一次函数 的图象交于
的图象交于 ,
, 两点. C
两点. C 为二次函数图象的顶点.
为二次函数图象的顶点.
(1)求二次函数 的解析式;
的解析式;
(2)定义函数f:“当自变量x任取一值时,x对应的函数值分别为y1或y2,若y1≠y2,函数f的函数值等于y1、y2中的较小值;若y1=y2,函数f的函数值等于y1(或y2).” 当直线 (k >0)与函数f的图象只有两个交点时,求
(k >0)与函数f的图象只有两个交点时,求 的值.
的值.
(1)y=x2-2x+1;(2)k=1,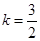 ,
,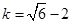 .
.
解析试题分析:(1)根据题意设抛物线的解析式为y=a(x-1)2,把A(0,1)代入求出a的值即可.
(2)根据题意可知直线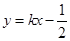 (k >0)与函数f的图象只有两个交点共有三种情况:①直线
(k >0)与函数f的图象只有两个交点共有三种情况:①直线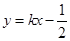 与直线AB:y=x+1平行,②直线
与直线AB:y=x+1平行,②直线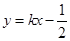 过点B(3,4),③直线
过点B(3,4),③直线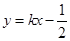 与二次函数y=x2-2x+1的图象只有一个交点,分别求出k的值即可.
与二次函数y=x2-2x+1的图象只有一个交点,分别求出k的值即可.
试题解析:(1)设抛物线解析式为y=a(x-1)2,,
由抛物线过点A(0,1),可得y=x2-2x+1
(2)可得B(3,4)
直线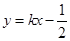 (k >0)与函数f的图象只有两个交点共有三种情况:
(k >0)与函数f的图象只有两个交点共有三种情况:
①直线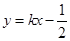 与直线AB:y=x+1平行,此时k=1;
与直线AB:y=x+1平行,此时k=1;
②直线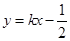 过点B(3,4),此时
过点B(3,4),此时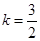 ;
;
③直线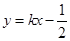 与二次函数y=x2-2x+1的图象只有一个交点,
与二次函数y=x2-2x+1的图象只有一个交点,
此时有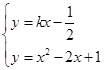 得
得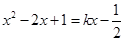 ,
,
由△=0可得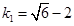 ,
,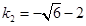 .
.
综上:k=1,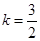 ,
,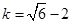 .
.
考点:二次函数综合题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
某服装经营部每天的固定费用为300元,现试销一种成本为每件80元的服装.规定试销期间销售单价不低于成本单价,且获利不得高于35%.经试销发现,每件销售单价相对成本提高x(元)(x为整数)与日均销售量y(件)之间的关系符合一次函数y=kx+b,且当x=10时,y=100;x=20时,y=80.
(1)求一次函数y=kx+b的关系式;
(2)设该服装经营部日均获得毛利润为W元(毛利润=销售收入-成本-固定费用),求W关于x的函数关系式;并求当销售单价定为多少元时,日均毛利润最大,最大日均毛利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知二次函数y=a(x-m)2-2a(x-m)(a,m为常数,且a≠0).
(1)求证:不论a与m为何值,该函数的图象与x轴总有两个公共点;
(2)设该函数的图象的顶点为C,与x轴交于A,B两点,当△ABC是等腰直角三角形时,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图所示,某居民小区要在一块一边靠墙(墙长15m)的空地上修建一个矩形花园ABCD,花园的一边靠墙,另三边用总长为40m的栅栏围成,若花园的BC边长为x米,花园的面积为y(m2)
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)满足条件的花园面积能达到200m2吗?若能,求出此时x的值;若不能,说明理由;
(3)请结合题意,判断当x取何值时,花园的面积最大?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
在2014年“元旦”前夕,某商场试销一种成本为30元的文化衫,经试销发现,若每件按34元的价格销售,每天能卖出36件;若每件按39元的价格销售,每天能卖出21件.假定每天销售件数y(件)是销售价格x(元)的一次函数.
(1)直接写出y与x之间的函数关系式y= .
(2)在不积压且不考虑其他因素的情况下,每件的销售价格定为多少元时,才能使每天获得的利润P最大?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某宾馆有50个房间供游客住宿,当每个房间的房价为每天180元时,房间会全部住满.当每个房间每天的房价每增加10元时,就会有一个房间空闲.宾馆需对游客居住的每个房间每天支出20元的各种费用.根据规定,每个房间每天的房价不得高于340元.设每个房间的房价每天增加x元(x为10的整数倍).
(1)设一天订住的房间数为y,直接写出y与x的函数关系式及自变量x的取值范围;
(2)设宾馆一天的利润为w元,求w与x的函数关系式;
(3)一天订住多少个房间时,宾馆的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
为了落实国务院的指示精神,某地方政府出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:y=﹣2x+80.设这种产品每天的销售利润为w元.
(1)求w与x之间的函数关系式.
(2)该产品销售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种产品的销售价不高于每千克28元,该农户想要每天获得150元的销售利润,销售价应定为每千克多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在边长为24cm的正方形纸片ABCD上,剪去图中阴影部分的四个全等的等腰直角三角形,再沿图中的虚线折起,折成一个长方体形状的包装盒(A、B、C、D四个顶点正好重合于上底面上一点)。已知E、F在AB边上,是被剪去的一个等腰直角三角形斜边的两个端点,设AE=BF=x(cm).
(1)若折成的包装盒恰好是个正方体,试求这个包装盒的体积V;
(2)某广告商要求包装盒的表面(不含下底面)面积S最大,试问x应取何值?S最大值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com