
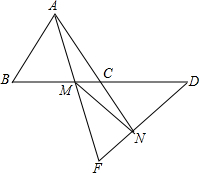
 等边△ABC,延长BC至D,使得CD=BC,M为BC一点,F为AM延长线一点,且∠AFD=60°,射线AC交DF于N,求证:AM=MN.
等边△ABC,延长BC至D,使得CD=BC,M为BC一点,F为AM延长线一点,且∠AFD=60°,射线AC交DF于N,求证:AM=MN. 分析 作辅助线,构建全等三角形,根据两个三角形有两个角分别相等,则第三个角相等,得∠BAM=∠FDM,证明△ABM≌△DCN,得BM=CN,根据等边△MHC,证明△AHM≌△NCM,得出结论AM=MN.
解答 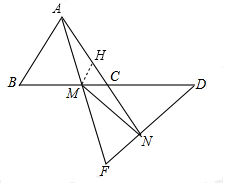 证明:∵△ABC是等边三角形,
证明:∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,AC=BC=AB,
在△ABM和△FMD中,
∵∠ABC=∠AFD=60°,∠AMB=∠FMD,
∴∠BAM=∠FDM,
∵∠ABC=∠NCD=60°,DC=BC=AB,
∴△ABM≌△DCN,
∴BM=CN,
过M作MH∥AB,交AC于H,
∴∠HMC=∠ABC=60°,
∵∠ACB=60°,
∴∠MHC=60°,
∴△MHC是等边三角形,
∴MC=MH=CH,
∵AC=BC,
∴AC-HC=BC-CM,
即AH=BM,
∴AH=CN,
∵∠AHM=180°-60°=120°,
∠MCN=180°-60°=120°,
∴∠AHM=∠MCN,
∴△AHM≌△NCM,
∴AM=MN.
点评 本题考查了等边三角形和全等三角形的性质和判定,作辅助线,构建△AHM和△NCM,证明△AHM≌△NCM是关键,本题多次运用了等边三角形的性质:各边相等且每个角为60°;为三角形全等创造条件,从而得出结论.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
| 日 | 一 | 二 | 三 | 四 | 五 | 六 |
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
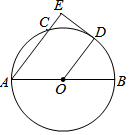 如图,AB为⊙O的直径,点C为⊙O上的一点,点D是$\widehat{BC}$的中点,过D作⊙O的切线交AC于E,DE=3,CE=1.
如图,AB为⊙O的直径,点C为⊙O上的一点,点D是$\widehat{BC}$的中点,过D作⊙O的切线交AC于E,DE=3,CE=1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com