
【题目】如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y= ![]() (k>0)的图象与BC边交于点E.
(k>0)的图象与BC边交于点E.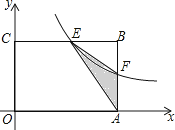
(1)当F为AB的中点时,求该函数的解析式;
(2)当k为何值时,△EFA的面积最大,最大面积是多少?
【答案】
(1)
解:∵在矩形OABC中,OA=3,OC=2,
∴B(3,2),
∵F为AB的中点,
∴F(3,1),
∵点F在反比例函数y= ![]() (k>0)的图象上,
(k>0)的图象上,
∴k=3,
∴该函数的解析式为y= ![]() (x>0)
(x>0)
(2)
解:由题意知E,F两点坐标分别为E( ![]() ,2),F(3,
,2),F(3, ![]() ),
),
∴S△EFA= ![]() AFBE=
AFBE= ![]() ×
× ![]() k(3﹣
k(3﹣ ![]() k),
k),
= ![]() k﹣
k﹣ ![]() k2
k2
=﹣ ![]() (k2﹣6k+9﹣9)
(k2﹣6k+9﹣9)
=﹣ ![]() (k﹣3)2+
(k﹣3)2+ ![]()
当k=3时,S有最大值.
S最大值= ![]()
【解析】(1)当F为AB的中点时,点F的坐标为(3,1),由此代入求得函数解析式即可;(2)根据图中的点的坐标表示出三角形的面积,得到关于k的二次函数,利用二次函数求出最值即可.此题属于反比例函数综合题,涉及的知识有:坐标与图形性质,待定系数法确定反比例解析式,以及二次函数的性质,熟练掌握待定系数法是解本题的关键.
【考点精析】认真审题,首先需要了解二次函数的最值(如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a).


科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c经过A(﹣1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴.
(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当△PAC的周长最小时,求点P的坐标;
(3)在直线l上是否存在点M,使△MAC为等腰三角形?若存在,直接写出所有符合条件的点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相交于点D,E,F,⊙O是△BEF的外接圆,∠EBF的平分线交EF于点G,交⊙O于点H,连接BD、FH.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作正方形ADEF,连接CF.
(1)观察猜想
如图1,当点D在线段BC上时,
①BC与CF的位置关系为: .
②BC,CD,CF之间的数量关系为:;(将结论直接写在横线上)
(2)数学思考
如图2,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
(3)拓展延伸
如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE.若已知AB=2 ![]() ,CD=
,CD= ![]() BC,请求出GE的长.
BC,请求出GE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为米(结果精确到0.1米,参考数据: ![]() =1.41,
=1.41, ![]() =1.73).
=1.73).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的切线,B为切点,AC经过点O,与⊙O分别相交于点D,C.若∠ACB=30°,AB= ![]() ,则阴影部分的面积是( )
,则阴影部分的面积是( ) 
A.![]()
B.![]()
C.![]() ﹣
﹣ ![]()
![]()
D.![]() ﹣
﹣ ![]()
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校九年级学生的身高情况,随机抽取部分学生的身高进行调查,利用所得数据绘成如图统计图表:
频数分布表
身高分组 | 频数 | 百分比 |
x<155 | 5 | 10% |
155≤x<160 | a | 20% |
160≤x<165 | 15 | 30% |
165≤x<170 | 14 | b |
x≥170 | 6 | 12% |
总计 | 100% |
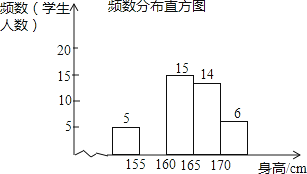
(1)填空:a= , b=;
(2)补全频数分布直方图;
(3)该校九年级共有600名学生,估计身高不低于165cm的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了让书籍开拓学生的视野,陶冶学生的情操,向阳中学开展了“五个一”课外阅读活动,为了解全校学生课外阅读情况,抽样调查了50名学生平均每天课外阅读时间(单位:min),将抽查得到的数据分成5组,下面是尚未完成的频数、频率分布表:
组别 | 分组 | 频数(人数) | 频率 |
1 | 10≤t<30 | ① | 0.16 |
2 | 30≤t<50 | 20 | ② |
3 | 50≤t<70 | ③ | 0.28 |
4 | 70≤t<90 | 6 | ④ |
5 | 90≤t<110 | ⑤ | ⑥ |
(1)将表中空格处的数据补全,完成上面的频数、频率分布表;
(2)请在给出的平面直角坐标系中画出相应的频数直方图;
(3)如果该校有1500名学生,请你估计该校共有多少名学生平均每天阅读时间不少于50min?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形OABC的OA边在x轴的正半轴上,OC在y轴的正半轴上,抛物线y=ax2+bx经过点B(1,4)和点E(3,0)两点.
(1)求抛物线的解析式;
(2)若点D在线段OC上,且BD⊥DE,BD=DE,求D点的坐标;
(3)在条件(2)下,在抛物线的对称轴上找一点M,使得△BDM的周长为最小,并求△BDM周长的最小值及此时点M的坐标;
(4)在条件(2)下,从B点到E点这段抛物线的图象上,是否存在一个点P,使得△PAD的面积最大?若存在,请求出△PAD面积的最大值及此时P点的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com