
【题目】如图,△ABC内接于⊙O,AB为直径,作OD⊥AB交AC于点D,延长BC,OD交于点F,过点C作⊙O的切线CE,交OF于点E.
(1)求证:EC=ED;
(2)如果OA=4,EF=3,求弦AC的长.
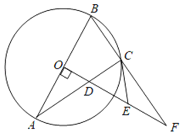
【答案】(1)见解析;(2)![]()
【解析】
(1)连接OC,由切线的性质可证得∠ACE+∠A=90°,又∠CDE+∠A=90°,可得∠CDE=∠ACE,则结论得证;
(2)先根据勾股定理求出OE,OD,AD的长,证明Rt△AOD∽Rt△ACB,得出比例线段即可求出AC的长.
(1)证明:连接OC,
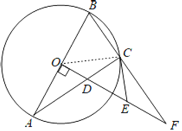
∵CE与⊙O相切,OC是⊙O的半径,
∴OC⊥CE,
∴∠OCA+∠ACE=90°,
∵OA=OC,
∴∠A=∠OCA,
∴∠ACE+∠A=90°,
∵OD⊥AB,
∴∠ODA+∠A=90°,
∵∠ODA=∠CDE,
∴∠CDE+∠A=90°,
∴∠CDE=∠ACE,
∴EC=ED;
(2)∵AB为⊙O的直径,
∴∠ACB=90°,
在Rt△DCF中,∠DCE+∠ECF=90°,∠DCE=∠CDE,
∴∠CDE+∠ECF=90°,
∵∠CDE+∠F=90°,
∴∠ECF=∠F,
∴EC=EF,
∵EF=3,
∴EC=DE=3,
∴OE=5,
∴OD=OE﹣DE=2,
在Rt△OAD中,AD=![]() ,
,
在Rt△AOD和Rt△ACB中,
∵∠A=∠A,∠ACB=∠AOD,
∴Rt△AOD∽Rt△ACB,
∴![]() ,即
,即![]() ,
,
∴AC=![]() .
.


科目:初中数学 来源: 题型:
【题目】解放碑某商场地下停车场有5个出入口,每天早晨7点开始对外停车且此时车位空置率为80%,在每个出入口的车辆数均是匀速出入的情况下,如果开放2个进口和3个出口,7小时车库恰好停满:如果开放3个进口和2个出口,4小时车库恰好停满.2019年清明节期间,由于商场人数增多,早晨7点时的车位空置率变为60%,又因为车库改造,只能开放2个进口和1个出口,则从早晨7点开始经过_______小时车库恰好停满.
查看答案和解析>>
科目:初中数学 来源: 题型:
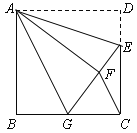
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.
(1)求证:①△ABG≌△AFG; ②BG=GC;
(2)求△FGC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y4x4与x轴,y轴分别交于点A,B,点A在抛物线yax2bx3a(a0)上,将点B向右平移3个单位长度,得到点C.
(1)抛物线的顶点坐标为 (用含a的代数式表示)
(2)若a1,当t-1≤x≤t时,函数yax2bx3a(a0)的最大值为y1,最小值为y2,且y1y22,求t的值;
(3)若抛物线与线段BC恰有一个公共点,结合函数图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2016年泉州市初中体育中考中,随意抽取某校5位同学一分钟跳绳的次数分别为:158,160,154,158,170,则由这组数据得到的结论错误的是( )
A. 平均数为160 B. 中位数为158 C. 众数为158 D. 方差为20.3
查看答案和解析>>
科目:初中数学 来源: 题型:
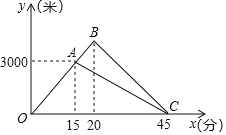
【题目】张琪和爸爸到曲江池遗址公园运动,两人同时从家出发,沿相同路线前行,途中爸爸有事返回,张琪继续前行5分钟后也原路返回,两人恰好同时到家张琪和爸爸在整个运动过程中离家的路点y1(米),y2(米)与运动时间x(分)之间的函数关系如图所示
(1)求爸爸返问时离家的路程y2(米)与运动时间x(分)之间的函数关系式;
(2)张琪开始返回时与爸爸相距多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
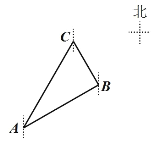
【题目】在一次夏令营中,小亮从位于![]() 点的营地出发,沿北偏东60°方向走了
点的营地出发,沿北偏东60°方向走了![]() 到达
到达![]() 地,然后再沿北偏西30°方向走了若干千米到达
地,然后再沿北偏西30°方向走了若干千米到达![]() 地,测得
地,测得![]() 地在
地在![]() 地南偏西30°方向,则
地南偏西30°方向,则![]() 、
、![]() 两地的距离为_________
两地的距离为_________![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线C1:y=a(x+2)2-5的顶点为P,与x轴相交于A、B两点(点A在点B的左边),点B的横坐标是1.
(1) 求P点坐标及a的值;
(2)如图(1),
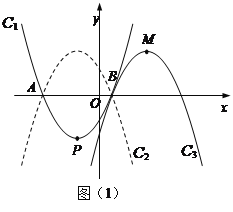
抛物线C2与抛物线C1关于x轴对称,将抛物线C2向右平移,平移后的抛物线记为C3,C3的顶点为M,当点P、M关于点B成中心对称时,求C3的解析式;
(3) 如图(2),
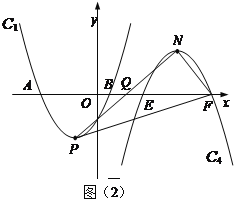
点Q是x轴正半轴上一点,将抛物线C1绕点Q旋转180°后得到抛物线C4.抛物线C4的顶点为N,与x轴相交于E、F两点(点E在点F的左边),当以点P、N、F为顶点的三角形是直角三角形时,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣x+3与x轴、y轴分别交于B、C两点,抛物线y=﹣x2+bx+c经过B、C两点,与x轴另一交点为A,顶点为D.
(1)求抛物线的解析式;
(2)在x轴上找一点E,使△EDC的周长最小,求符合条件的E点坐标;
(3)在抛物线的对称轴上是否存在一点P,使得∠APB=∠OCB?若存在,求出PB2的值;若不存在,请说明理由.
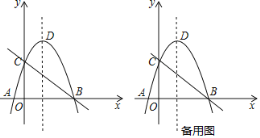
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com