D
分析:求出∠DOC=60°,根据矩形性质求出OA=OB,得出等边三角形OAB,求出OA=OB=AB,设AB=OB=a,则BD=2OA=2a,根据勾股定理求出AD,即可求出答案.
解答:

∵∠AOD=120°,
∴∠DOC=60°,
∵四边形ABCD是矩形,
∴∠DAB=90°,AC=2OA=2OC,BD=2OD=2OB,AC=BD,
∴OA=OC=OB=OD,
∴△OAB是等边三角形,
∴OA=OB=AB,
设AB=OB=a,则BD=2OA=2a,
在Rt△BAD中,由勾股定理得:AD=
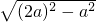
=

a,
∴AB:AD=1:

,
故选D.
点评:本题考查了等边三角形的性质和判定,矩形的性质,注意:矩形的对角线相等且互相平分.




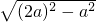 =
= a,
a, ,
,
