Question

14．在△ABC中，∠ACB=90°经过点B的直线l（l不与直线AB重合）与直线BC的夹角等于∠ABC，分别过点C、A做直线l的垂线，垂足分别为点D、E．
（1）问题发现
①若∠ABC=30°，如图①，则$\frac{CD}{AE}$=$\frac{1}{2}$；
②∠ABC=45°，如图②，则$\frac{CD}{AE}$=$\frac{1}{2}$；
（2）拓展探究
当0°＜∠ABC＜90°，$\frac{CD}{AE}$的值有无变化？请仅就图③的情形给出证明．
（3）问题解决
若直线CE、AB交于点F，$\frac{CF}{EF}$=$\frac{5}{6}$，CD=4，请直接写出线段BD的长．

Answer 1

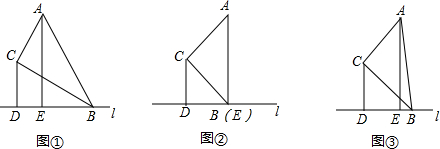
分析 （1）①根据直角三角形的性质得到CD=$\frac{1}{2}$BC，根据全等三角形的性质得到BC=AE，等量代换得到CD=$\frac{1}{2}$AE，即可得到结论；②如图②，推出△ACB是等腰直角三角形，求得∠CBD=45°，证得B与E重合，根据等腰直角三角形的性质得到EF=$\frac{1}{2}$AE根据矩形的性质得到EF=CD，与得到结论；
（2）如图③，延长AC与直线L交于G，根据等腰三角形的性质得到BA=BG，证得CD∥AE，根据相似三角形的性质得到$\frac{CD}{AE}=\frac{GC}{GA}=\frac{1}{2}$；
（3）①当点F在线段AB上时，过C作CG∥l交AE于H，交AB于G，推出△CFG∽△EFB，根据相似三角形的性质得到$\frac{CF}{EF}=\frac{CG}{BE}=\frac{5}{6}$，设CG=5x，BE=6x，则AB=10x，∵∠根据勾股定理得到AE=8x，由（2）得AE=2CD，根据相似三角形的性质得到$\frac{HG}{BE}=\frac{AH}{AE}=\frac{1}{2}$，于是得到CH=CG+HG=8，根据平行四边形的性质得到DE=CH=8，求得BD=DE=BE=2，②如图⑤，当点F在线段BA的延长线上时，过点C作CG∥l交AE于点G，交AB于H，同理可得求得结论．

解答 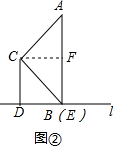解：（1）①∵CD⊥BD，
∴∠CDB=90°，
∵∠DBC=∠ABC=30°，
∴CD=$\frac{1}{2}$BC，
在△ABE与△ABC中，$\left\{\begin{array}{l}{∠ACB=∠AEB=90°}\\{∠BAE=∠ABC=30°}\\{AB=BA}\end{array}\right.$，
∴△ABC≌△ABE，
∴BC=AE，
∴CD=$\frac{1}{2}$AE，
∴$\frac{CD}{AE}$=$\frac{1}{2}$，
②如图②，∵∠ABC=45°∠ACB=90°，
∴△ACB是等腰直角三角形，
∵∠CBD=45°，
∴∠ABD=90°，
∵AE⊥BC，
∴B与E重合，
∴EF=$\frac{1}{2}$AE，
∵CD⊥BD，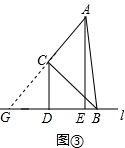
∴四边形CDEF的矩形，
∴EF=CD，
∴CD=$\frac{1}{2}$AE，
∴$\frac{CD}{AE}$=$\frac{1}{2}$；
故答案为：$\frac{1}{2}$，$\frac{1}{2}$；

（2）$\frac{CD}{AE}$的值有无变化，
理由：如图③，延长AC与直线L交于G，
∴∠ABC=∠CBG，
∵∠ACB=90°，
∴∠AGB=∠BAG，
∴BA=BG，
∵AE⊥l，CD⊥l，
∴CD∥AE，
∴△GCD∽△GAE，
∴$\frac{CD}{AE}=\frac{GC}{GA}=\frac{1}{2}$；

（3）①当点F在线段AB上时，过C作CG∥l交AE于H，交AB于G，
∴∠DBC=∠HCB，
∵∠DBC=∠CBF，
∴∠CBF=∠HCB，
∴CG=BG，
∵∠ACB=90°，
∴∠CAG+∠CBF=∠HCB+∠ACG=90°，
∴∠ACG=∠CAG，
∴CG=AG=BG，
∵CG∥l，
∴△CFG∽△EFB，
∴$\frac{CF}{EF}=\frac{CG}{BE}=\frac{5}{6}$，
设CG=5x，BE=6x，
则AB=10x，
∵∠AEB=90°，
∴AE=8x，
由（2）得AE=2CD，
∵CD=4，
∴AE=8，
∴x=1，
∴AB=10，BE=6，CG=5，
∵GH∥l，
∴△AGH∽△ABE，
∴$\frac{HG}{BE}=\frac{AH}{AE}=\frac{1}{2}$，
∴HG=3，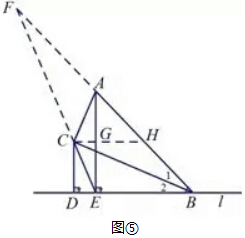
∴CH=CG+HG=8，
∵CG∥l，CD∥AE
∴四边形CDEH为平行四边形，
∴DE=CH=8，
∴BD=DE-BE=2，
②如图⑤，当点F在线段BA的延长线上时，过点C作CG∥l交AE于点G，交AB于H，同法可以假设CH=5y，EB=6y，
AB=10y，AE=8y，
∵AE=2CD=8，CH=5，EB=6，
∴y=1，易知GH=$\frac{1}{2}$EB=3，CG=DE=2，
∴DB=DE+EB=2+6=8，
，综上可得BD=2或8．

点评 本题考查了全等三角形的判定和性质，相似三角形的判定和性质，平行四边形的判定和性质，勾股定理，正确的作出辅助线构造相似三角形是解题的关键．