
【题目】以四边形ABCD的边AB,AD为边分别向外侧作等边三角形ABF和等边三角形ADE,连接EB,FD,交点为G.
(1)当四边形ABCD为正方形时,如图①,EB和FD的数量关系是 ;
(2)当四边形ABCD为矩形时,如图②,EB和FD具有怎样的数量关系?请加以证明;
(3)如图③,四边形ABCD由正方形到矩形再到一般平行四边形的变化过程中,EB和FD具有怎样的数量关系?请直接写出结论,无需证明.

【答案】(1)DF=BE;(2)EB=FD,证明见解析;(3)DF=BE
【解析】
(1)根据题意可得AB=AF,AD=AE,∠FAB=∠EAD,即可得∠FAD=∠EAB,则可证△AFD≌△AEB,可得BE=DF
(2)根据题意可得AB=AF,AD=AE,∠FAB=∠EAD,即可得∠FAD=∠EAB,则可证△AFD≌△AEB,可得BE=DF
(3)根据题意可得AB=AF,AD=AE,∠FAB=∠EAD,即可得∠FAD=∠EAB,则可证△AFD≌△AEB,可得BE=DF.
解:(1)∵四边形ABCD是正方形
∴AB=AD,∠BAD=90°
∵△BAF和△AED是等边三角形
∴AF=AB,AD=AE,∠FAB=∠EAD=60°
∴AE=AD=AF=AB,∠FAD=∠EAB
∴△ABE≌△ADF
∴DF=BE
故答案为DF=BE
(2)EB=FD
理由如下:
∵△BAF和△AED是等边三角形
∴AF=AB,AD=AE,∠FAB=∠EAD=60°
∴∠FAB+∠BAD=∠EAD+∠BAD
∴∠FAD=∠EAB
又∵AF=AB,AE=AD
∴△ABE≌△AFD
∴DF=BE
(3)BE=DF
理由如下∵△BAF和△AED是等边三角形
∴AF=AB,AD=AE,∠FAB=∠EAD=60°
∴∠FAB+∠BAD=∠EAD+∠BAD
∴∠FAD=∠EAB
又∵AF=AB,AE=AD
∴△ABE≌△AFD
∴DF=BE


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 内部有若干个点,用这些点以及正方形
内部有若干个点,用这些点以及正方形![]() 的顶点
的顶点![]() 、
、![]() 、
、![]() 、
、![]() 把原正方形分割成一些三角形(互相不重叠)
把原正方形分割成一些三角形(互相不重叠)
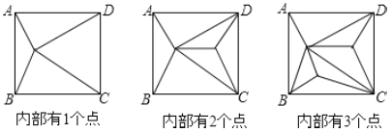
(1)填写下表:
正方形 | 1 | 2 | 3 | 4 | … |
|
分割成的三角形的个数 | 4 | 6 | ______ | ______ | … | ______ |
(2)如果原正方形内有101个点,此时原正方形被分割成多少个三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OM是∠AOC的平分线,ON是∠BOC的平分线.
(1)如图1,当∠AOB是直角,∠BOC=60°时,∠MON的度数是多少?
(2)如图2,当∠AOB=α,∠BOC=60°时,猜想∠MON与α的数量关系;
(3)如图3,当∠AOB=α,∠BOC=β时,猜想∠MON与α、β有数量关系吗?如果有,指出结论并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用粗线在数轴上表示了一个“范围”,这个“范围”包含所有大于1且小于2的数(数轴上1与2这两个数的点空心,表示这个范围不包含数1和2).
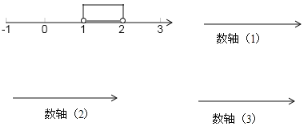
请你在数轴上表示出一个范围,使得这个范围:
(1)包含所有大于-3且小于0的数[画在数轴(1)上];
(2)包含![]() 这两个数,且只含有5个整数[画在数轴(2)上];
这两个数,且只含有5个整数[画在数轴(2)上];
(3)同时满足以下三个条件:[画在数轴(3)上]
①至少有100对互为相反数和100对互为倒数;
②有最小的正整数;
③这个范围内最大的数与最小的数表示的点的距离大于3但小于4.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着通讯技术迅猛发展,人与人之间的沟通方式更多样、便捷.某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:

(1)这次统计共抽查了 名学生;在扇形统计图中,表示“QQ”的扇形圆心角的度数为 ;
(2)将条形统计图补充完整;
(3)该校共有1500名学生,请估计该校最喜欢用“微信”进行沟通的学生有多少名?
(4)某天甲、乙两名同学都想从“微信”、“QQ”、“电话”三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选中同一种沟通方式的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某书店准备购进甲、乙两种图书共100本,购书款不高于2224元,预这100本图书全部售完的利润不低于1100元,两种图书的进价、售价如表所示:
甲种图书 | 乙种图书 | |
进价(元/本) | 16 | 28 |
售价(元/本) | 26 | 40 |
请回答下列问题:
(1)书店有多少种进书方案?
(2)在这批图书全部售出的条件下,(1)中的哪种方案利润最大?最大利润是多少?(请你用所学的函数知识来解决)
查看答案和解析>>
科目:初中数学 来源: 题型:
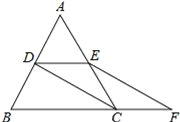
【题目】如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,过E点作EF∥DC交BC的延长线于点F,连接CD.
(1)求证:四边形CDEF是平行四边形;
(2)求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为8,B是数轴上位于点A左侧一点,且AB=20,
(1)写出数轴上点B表示的数 ;
(2)|5﹣3|表示5与3之差的绝对值,实际上也可理解为5与3两数在数轴上所对的两点之间的距离.如|x﹣3|的几何意义是数轴上表示有理数x的点与表示有理数3的点之间的距离.试探索:
①:若|x﹣8|=2,则x= .
②:|x+12|+|x﹣8|的最小值为 .
(3)动点P从O点出发,以每秒5个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.求当t为多少秒时?A,P两点之间的距离为2;
(4)动点P,Q分别从O,B两点,同时出发,点P以每秒5个单位长度沿数轴向右匀速运动,Q点以P点速度的两倍,沿数轴向右匀速运动,设运动时间为t(t>0)秒.问当t为多少秒时?P,Q之间的距离为4.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD相交于点O,OE平分∠AOD,OF⊥OC,
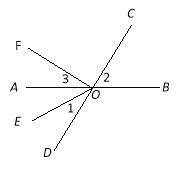
(1)图中∠AOF的余角是 (把符合条件的角都填出来);
(2)如果∠AOC=160°,那么根据 可得∠BOD= 度;
(3)如果∠1=32°,求∠2和∠3的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com