
分析 (1)根据欢喜数的定义可得出a+c=b,由$\overline{abc}$=100a+10b+c可得出$\overline{abc}$=99a+11b,结合b能被9整除即可证出“欢喜数$\overline{abc}$”能被99整除;
(2)设m=$\overline{{a}_{1}b{c}_{1}}$,n=$\overline{{a}_{2}b{c}_{2}}$(且a1>a2),根据F(m)-F(n)=(a1-a2)(b-a1-a2)=3结合a1、a2、b均为整数,即可得出a1-a2=1或a1-a2=3,将其代入m-n=99(a1-a2)中即可得出结论.
解答 (1)证明:∵$\overline{abc}$为欢喜数,
∴a+c=b.
∵$\overline{abc}$=100a+10b+c=99a+10b+a+c=99a+11b,b能被9整除,
∴11b能被99整除,99a能被99整除,
∴“欢喜数$\overline{abc}$”能被99整除.
(2)设m=$\overline{{a}_{1}b{c}_{1}}$,n=$\overline{{a}_{2}b{c}_{2}}$(且a1>a2),
∵F(m)-F(n)=a1•c1-a2•c2=a1•(b-a1)-a2(b-a2)=(a1-a2)(b-a1-a2)=3,a1、a2、b均为整数,
∴a1-a2=1或a1-a2=3.
∵m-n=100(a1-a2)-(a1-a2)=99(a1-a2),
∴m-n=99或m-n=297.
∴若F(m)-F(n)=3,则m-n的值为99或297.
点评 本题考查了因式分解的应用,解题的关键是:(1)找出$\overline{abc}$=99a+11b;(2)由F(m)-F(n)=3,求出a1-a2=1或a1-a2=3.


 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
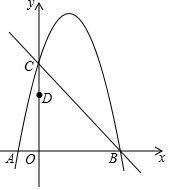 如图,抛物线y=-x2+bx+c经过直线y=-x+5与坐标轴的交点B,C.已知D(0,3).
如图,抛物线y=-x2+bx+c经过直线y=-x+5与坐标轴的交点B,C.已知D(0,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
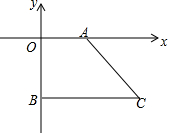 如图,在平面直角坐标系中,A(a,0)是x轴正半轴上一点,C是第四象限一点,CB⊥y轴,交y轴负半轴于点B(0,b),且(a-3)2+|b+4|=0,S四边形AOBC=16,求C点坐标.
如图,在平面直角坐标系中,A(a,0)是x轴正半轴上一点,C是第四象限一点,CB⊥y轴,交y轴负半轴于点B(0,b),且(a-3)2+|b+4|=0,S四边形AOBC=16,求C点坐标.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com