
| A. | 85 | B. | 88 | C. | 95 | D. | 100 |
分析 设期中的成绩是x分,期末的成绩是y分,设学期成绩是z,根据平均数公式和权平均数公式列出式子,然后对每个答案进行判断即可.
解答 解:设期中的成绩是x分,期末的成绩是y分,
则$\frac{x+y}{2}$=90,即x+y=180,
则3x+3y=540…①;
若学期成绩是z,则30%x+70%y=z,即3x+7y=10z…②,
②-①得4y=10z-540,
则y=$\frac{10z-540}{4}$,
当z=85时,y=77.5,则x=180-72.5=102.5>100(分),不满足条件,则A错误;
当z=88时,y=85,则x=180-85=95(分),满足条件,则B正确;
当z=95时,y=102.5>0,则不满足条件,故C错误;
当=z=100时,y=115>0,不满足条件,故D错误.
故选B.
点评 本题考查了加权平均数公式,数据的权能够反映数据的相对“重要程度”,要突出某个数据,只需要给它较大的“权”,权的差异对结果会产生直接的影响.对于一组不同权重的数据,加权平均数更能反映数据的真实信息,理解公式是关键.


科目:初中数学 来源: 题型:解答题
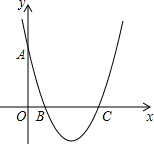 如图,对称轴为直线x=2的抛物线y=ax2+bx+c(a≠0)与x轴相交于B,C两点,其中B点坐标为(1,0),与y轴交于点A,A点坐标为(0,3)
如图,对称轴为直线x=2的抛物线y=ax2+bx+c(a≠0)与x轴相交于B,C两点,其中B点坐标为(1,0),与y轴交于点A,A点坐标为(0,3)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在矩形ABCD中,BC=2,M为对角线BD的中点,连接CM,以CM为直径作⊙O交BD于点E,连接AE,当直线AE与⊙O相切时,AB的长为$\sqrt{6}$-$\sqrt{2}$.
如图,在矩形ABCD中,BC=2,M为对角线BD的中点,连接CM,以CM为直径作⊙O交BD于点E,连接AE,当直线AE与⊙O相切时,AB的长为$\sqrt{6}$-$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
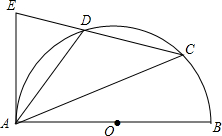 如图,AB是半圆⊙O的直径,点C是半圆上一个动点(不与点A,B重合),点D是弧AC的中点,延长CD交经过点A的切线于点E,连接AD,当△ADE是等腰三角形时,求∠BAC的度数.
如图,AB是半圆⊙O的直径,点C是半圆上一个动点(不与点A,B重合),点D是弧AC的中点,延长CD交经过点A的切线于点E,连接AD,当△ADE是等腰三角形时,求∠BAC的度数.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com