
分析 (1)利用点到坐标轴的距离的特点即可得出结论;
(2)先找出a-b=5,进而根据平移的性质,得出AA'=BB',再用面积公式即可求出点B平移后的坐标;
(3)先得出b=a-5,c=a+2,分两种情况,利用面积的和差表示出三角形ABC的面积,进而建立不等式求解即可.
解答 解:(1)点C的坐标为(c,d)且到x轴的距离为6,
∴|d|=6,
∴d=±6,
故答案为:±6;
(2)如图1,
∵$\left\{\begin{array}{l}{a-2b+c=12①}\\{2a-b-c=3②}\end{array}\right.$
∴①+②得,3a-3b=15,
∴a-b=5,
∴b=a-5;
∴AD=a-b=5,
①+2×②得,3a-3c=-6,
∴a-c=-2,
∴c=a+2
∵B(b,2),
∴BD=2,
设平移后B的对应点B'(b,m),
∴AA'=BB'=|m-2|,B'D=|m|,
∵线段AB扫过的面积为15,
∴15=S梯形AA'B'D-S△ABD=$\frac{1}{2}$(AA'+B'D)•AD-$\frac{1}{2}$AD•BD=$\frac{1}{2}$(|m-2|+|m|)×5-$\frac{1}{2}$×5×|m|=$\frac{5}{2}$|m-2|,
∴m=8或m=-4,
∴平移后B点的坐标B'的纵坐标为8或-4;
(3)如图2,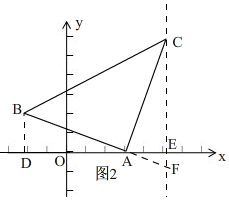
①当点C在直线AB上时,
过点B作BD⊥x轴于D,过点C作CF⊥x轴交x轴于E,BA的延长线于F;
∴BD∥EF,
∴△ADB∽△AEF,
∴$\frac{BD}{EF}=\frac{AD}{AE}$,
∴EF=$\frac{BD•AE}{AD}$=$\frac{2×2}{5}$=$\frac{4}{5}$,
∴d>-$\frac{4}{5}$,
∴4+5d>0,
由(2)知,c-a=2,
∴AE=2,
∴DE=AD+AE=7,BD=2,
∵C(c,d),
∴CE=|d|,
∴S△ABC=S梯形BDEC-S△ABD-S△ACE
=$\frac{1}{2}$(BD+CE)×DE-$\frac{1}{2}$AD×BD-$\frac{1}{2}$AE×CE
=$\frac{1}{2}$[(2+|d|)×7-5×2-2×|d|]
=$\frac{1}{2}$(14+7|d|-10-2|d|)
=$\frac{1}{2}$(4+5|d|)
=2+$\frac{5}{2}$d,
∵△ABC的面积小于等于10,
∴0<S△ABC≤10,
∴0<2+$\frac{5}{2}$d≤10,
∴-$\frac{4}{5}$<d≤$\frac{16}{5}$;
②当点C在直线AB下方时,即:d<-$\frac{4}{5}$,如图3,
过点B作BD⊥x轴于D,过点C作CF⊥x轴交x轴于E,过点B作BF⊥CE于F,
S△ABC=S△BCF-S梯形AEFB-S△ACE
=$\frac{1}{2}$CE•BF-$\frac{1}{2}$(AE+BF)•BD-$\frac{1}{2}$AE•CE
=$\frac{1}{2}$[CF•BF-(AE+BF)•BD-AE•CE]
=$\frac{1}{2}$[(2-d)×7-(2+7)×2-2(-d)]
=$\frac{1}{2}$(-5d-4)
=-$\frac{5}{2}$d-2
∵△ABC的面积小于等于10,
∴0<S△ABC≤10,
∴0<-$\frac{5}{2}$d-2≤10,
∴-$\frac{24}{5}$≤d<-$\frac{4}{5}$;
即:d的取值范围为-$\frac{24}{5}$≤d≤$\frac{16}{5}$且d≠-$\frac{4}{5}$.
点评 此题是三角形综合题,主要考查了平移的性质,几何图形面积的计算方法,相似三角形的判定和性质,解本题的关键是得出b=a-5,c=a+2,是一道很好的中考题目.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:选择题
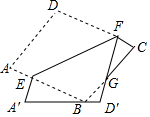 如图所示,在四边纸片ABCD中,AD∥BC,AB∥CD,将纸片沿EF折叠,点A,D分别落在A',D'处,且A'D'经过点B,FD'交BC于点G,连结EG,若EG平分∠FEB,EG∥A'D',∠D'FC=80°,则∠A的度数是( )
如图所示,在四边纸片ABCD中,AD∥BC,AB∥CD,将纸片沿EF折叠,点A,D分别落在A',D'处,且A'D'经过点B,FD'交BC于点G,连结EG,若EG平分∠FEB,EG∥A'D',∠D'FC=80°,则∠A的度数是( )| A. | 65° | B. | 70° | C. | 75° | D. | 80° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 近年来,我国很多地区持续出现雾霾天气,某市记者为了了解“雾霾天气的主要成因”,随机调查了该市部分市民,并对调查结果进行整理,绘制了如下尚不完整的统计图表.
近年来,我国很多地区持续出现雾霾天气,某市记者为了了解“雾霾天气的主要成因”,随机调查了该市部分市民,并对调查结果进行整理,绘制了如下尚不完整的统计图表.| 组别 | 观点 | 频数 |
| A | 大气气压低,空气不流动 | m |
| B | 地面灰尘大,空气湿度低 | 20 |
| C | 汽车尾气排放 | n |
| D | 工厂造成的污染 | 80 |
| E | 其他 | 30 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
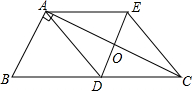 如图,在Rt△ABC中,∠BAC=90°,AD是BC边上的中线,过点D作BA的平行线交AC于点O,过点A作BC的平行线交DO的延长线于点E,连接CE.
如图,在Rt△ABC中,∠BAC=90°,AD是BC边上的中线,过点D作BA的平行线交AC于点O,过点A作BC的平行线交DO的延长线于点E,连接CE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com