
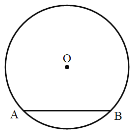
【题目】如图,在半径为4的⊙O中,弦AB长为4![]() .
.
(1)求圆心O到弦AB的距离;
(2)若点C为⊙O上一点(不与点A,B重合),求∠ACB的度数.
【答案】(1)2![]() ;(2)45°或135°
;(2)45°或135°
【解析】
(1)过点O作OC⊥AB于点C,证出△OAB是等边三角形,继而求得∠AOB的度数,然后由三角函数的性质,求得点O到AB的距离;
(2)证出△ABO是等腰直角三角形得出∠AOB=90°.再分两种情况:点C在优弧![]() 上,则∠BCA=45°;点C在劣弧
上,则∠BCA=45°;点C在劣弧![]() 上,则∠BCA=
上,则∠BCA=![]() (360°-∠AOB)=135°;即可得出结果.
(360°-∠AOB)=135°;即可得出结果.
(1)过点O作OD⊥AB于点D,连接AO,BO.如图1所示:
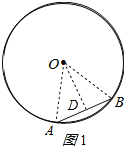
∵OD⊥AB且过圆心,AB=4![]() .,
.,
∴AD=![]() AB=2
AB=2![]() .,∠ADO=90°,
.,∠ADO=90°,
在Rt△ADO中,∠ADO=90°,AO=4,AD=2![]() .,
.,
∴OD=![]() =2
=2![]() .
.
即点O到AB的距离为2![]() .
.
(2)如图2所示:
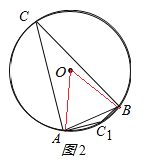
∵AO=BO=4,AB=4![]() ,
,
∴△ABO是等腰直角三角形,
∴∠AOB=90°.
若点C在优弧![]() 上,则∠BCA=45°;
上,则∠BCA=45°;
若点C在劣弧![]() 上,则∠BCA=
上,则∠BCA=![]() (360°-∠AOB)=135°;
(360°-∠AOB)=135°;
综上所述:∠BCA的度数为45°或135°.


科目:初中数学 来源: 题型:
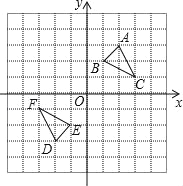
【题目】如图,△DEF是△ABC经过某种变换得到的图形,点A与点D,点B与点E,
点C与点F分别是对应点,观察点与点的坐标之间的关系,解答下列问题:
(1)分别写出点A与点D,点B与点E,点C与点F的坐标,并说说对应点的坐标有哪些特征;
(2)若点P(a+3,4﹣b)与点Q(2a,2b﹣3)也是通过上述变换得到的对应点,求a,b的值.
(3)求图中△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 为更新果树品种,某果园计划新购进A、B两个品种的果树苗栽植培育,若计划购进这两种果树苗共45棵,其中A种苗的单价为7元/棵,购买B种苗所需费用y(元)与购买数量x(棵)之间存在如图所示的函数关系.
(1)求y与x的函数关系式;
(2)若在购买计划中,B种苗的数量不超过35棵,但不少于A种苗的数量,请设计购买方案,使总费用最低,并求出最低费用.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,小聪同学利用直尺和圆规完成了如下操作:
,小聪同学利用直尺和圆规完成了如下操作:
①作![]() 的平分线
的平分线![]() 交
交![]() 于点
于点![]() ;
;
②作边![]() 的垂直平分线
的垂直平分线![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ;
;
③连接![]() ,
,![]() .
.
请你观察图形解答下列问题:

(1)线段![]() ,
,![]() ,
,![]() 之间的数量关系是________;
之间的数量关系是________;
(2)若![]() ,求
,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于![]() 的方程
的方程![]() .
.

![]() 求证:无论
求证:无论![]() 取任何实数时,方程总有实数根;
取任何实数时,方程总有实数根;
![]() 当二次函数
当二次函数![]() 的图象与
的图象与![]() 轴两个交点的横坐标均为整数,且
轴两个交点的横坐标均为整数,且![]() 为负整数时,求出函数的最大(或最小)值,并画出函数图象;
为负整数时,求出函数的最大(或最小)值,并画出函数图象;
![]() 若
若![]() ,
,![]() 是
是![]() 中抛物线上的两点,且
中抛物线上的两点,且![]() ,请你结合函数图象确定实数
,请你结合函数图象确定实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的周长为19,点D,E在边BC上,∠ABC的平分线垂直于AE,垂足为N,∠ACB的平分线垂直于AD,垂足为M,若BC=7,则MN的长度为( )

A. ![]() B. 2 C.
B. 2 C. ![]() D. 3
D. 3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com