
【题目】如图,反比例函数![]() 的图像经过点
的图像经过点![]() ,点
,点![]() ,连接
,连接![]() ,
,![]() ,若
,若![]() .
.
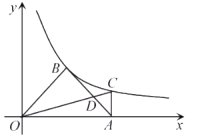
(1)求反比例函数的解析式;
(2)过点![]() 作
作![]() 轴,交反比例函数
轴,交反比例函数![]() 的图像于点
的图像于点![]() ,连接
,连接![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,
,![]() 轴,垂足为
轴,垂足为![]() ,通过
,通过![]() 可知E为OA中点,可求OE,在Rt△BEO中利用勾股定理可求BE,即可得到B点坐标,将B点代入解析式即可求得反比例函数解析式;
可知E为OA中点,可求OE,在Rt△BEO中利用勾股定理可求BE,即可得到B点坐标,将B点代入解析式即可求得反比例函数解析式;
(2)过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,
,![]() 轴,垂足为
轴,垂足为![]() ,可得四边形
,可得四边形![]() 为矩形,进而得到C点横坐标,根据C点在反比例函数图像上,可求C点坐标,结合点O(0,0)可求直线OC解析式;根据A、B两点坐标可求直线AB解析式,联立OC与AB两直线解析式即可求得点D坐标,再根据
为矩形,进而得到C点横坐标,根据C点在反比例函数图像上,可求C点坐标,结合点O(0,0)可求直线OC解析式;根据A、B两点坐标可求直线AB解析式,联立OC与AB两直线解析式即可求得点D坐标,再根据![]() 即可求得面积.
即可求得面积.
解:(1)过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,
,![]() 轴,垂足为
轴,垂足为![]() ,
,
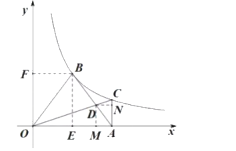
∴![]() ,
,
∴四边形![]() 为矩形,
为矩形,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 中
中![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]()
∴反比例函数的解析式为![]() ;
;
(2)过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,
,![]() 轴,垂足为
轴,垂足为![]() ,
,

同理,四边形![]() 为矩形,
为矩形,
∵![]() ,
,![]() 轴,
轴,
∴![]() 点横坐标为6,
点横坐标为6,
∴![]()
∴![]() ,
,![]() ,
,
设![]() 解析式为
解析式为![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
设![]() 解析式为
解析式为![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
解得: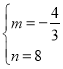 ,
,
∴![]() ,
,
∵点![]() 为
为![]() ,
,![]() 的交点,
的交点,
∴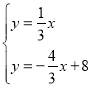 ,
,
解得: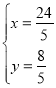 ,
,
∴![]() ,
,
∴![]()
∴![]() ,
,
∴![]()
∴![]() .
.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】“只要人人都献出一点爱,世界将变成美好的人间”,在新型肺炎疫情期间,全国人民万众一心,众志成城,共克时艰.某社区积极发起“援鄂捐款”活动倡议,有2500名居民踊跃参与献爱心.社区管理员随机抽查了部分居民捐款情况,统计图如图:

(1)计算本次共抽查居民人数,并将条形图补充完整;
(2)根据统计情况,请估计该社区捐款20元以上(含20元)的居民有多少人?
(3)该社区有1名男管理员和3名女管理员,现要从中随机挑选2名管理员参与“社区防控”宣讲活动,请用列表法或树状图法求出恰好选到“1男1女”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
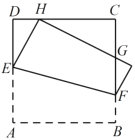
【题目】如图,将正方形![]() 折叠,使顶点
折叠,使顶点![]() 与
与![]() 边上的一点
边上的一点![]() 重合(
重合(![]() 不与端点
不与端点![]() ,
,![]() 重合),折痕交
重合),折痕交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,边
,边![]() 折叠后与边
折叠后与边![]() 交于点
交于点![]() ,设正方形
,设正方形![]() 的周长为
的周长为![]() ,
,![]() 的周长为
的周长为![]() ,则
,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.2
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于A,B两点(点A在点B左侧)
轴交于A,B两点(点A在点B左侧)
(1)求抛物线的顶点坐标(用含![]() 的代数式表示);
的代数式表示);
(2)求线段AB的长;
(3)抛物线与![]() 轴交于点C(点C不与原点
轴交于点C(点C不与原点![]() 重合),若
重合),若![]() 的面积始终小于
的面积始终小于![]() 的面积,求
的面积,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
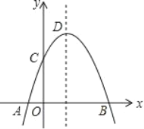
【题目】如图,抛物线y=﹣x2+2x+m+1交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个命题:
①当x>0时,y>0;
②若a=﹣1,则b=3;
③抛物线上有两点P(x1,y1)和Q(x2,y2),若x1<1<x2,且x1+x2>2,则y1>y2;
④点C关于抛物线对称轴的对称点为E,点G,F分别在x轴和y轴上,当m=2时,四边形EDFG周长的最小值为6![]() .
.
其中真命题的序号是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年3月24日,工信部发布《关于推动![]() 加快发展的通知》,全力推进
加快发展的通知》,全力推进![]() 网络建设、应用推广、技术发展和安全保障.工信部提出,要培育新型消费模式,加快用户向
网络建设、应用推广、技术发展和安全保障.工信部提出,要培育新型消费模式,加快用户向![]() 迁移,推动“
迁移,推动“![]() 医疗健康”创新发展,实施“
医疗健康”创新发展,实施“![]() 工业互联网”512工程,促进“
工业互联网”512工程,促进“![]() 车联网”协同发展,构建
车联网”协同发展,构建![]() 应用生态系统.现“
应用生态系统.现“![]() 网络”已成为一个热门词汇,某校为了解九年级学生对“
网络”已成为一个热门词汇,某校为了解九年级学生对“![]() 网络”的了解程度,对九年级学生行了一次测试(一共10道题答对1道得1分,满分10分),测试结束后随机抽取了部分学生的成绩整理分析,绘制出如图所示的两幅不完整的统计图,请根据图中信息解答下列问题:
网络”的了解程度,对九年级学生行了一次测试(一共10道题答对1道得1分,满分10分),测试结束后随机抽取了部分学生的成绩整理分析,绘制出如图所示的两幅不完整的统计图,请根据图中信息解答下列问题:
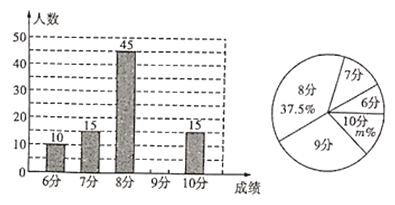
(1)请补全条形统计图,扇形统计图中![]() __;
__;
(2)所调查学生成绩的众数是_ ____分,平均数是_ 分;
(3)若该校九年级学生有![]() 人,请估计得分不少于
人,请估计得分不少于![]() 分的有多少人?
分的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
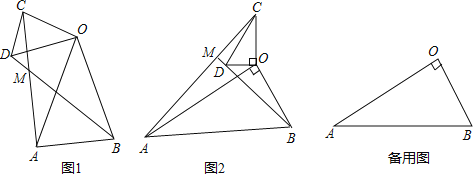
【题目】(1)问题发现
如图1,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=40°,连接AC,BD交于点M.填空:
①![]() 的值为 ;
的值为 ;
②∠AMB的度数为 .
(2)类比探究
如图2,在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC交BD的延长线于点M.请判断![]() 的值及∠AMB的度数,并说明理由;
的值及∠AMB的度数,并说明理由;
(3)拓展延伸
在(2)的条件下,将△OCD绕点O在平面内旋转,AC,BD所在直线交于点M,若OD=1,OB=![]() ,请直接写出当点C与点M重合时AC的长.
,请直接写出当点C与点M重合时AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com