练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    把正方形ABCD沿对角线AC的方向移动到A1B1C1D1的位置，它们重叠部分的面积是正方形ABCD的面积的一半，若AC=
    		2
    ，则平移的距离是
     
    ．
    考点：平移的性质,相似三角形的判定与性质
    专题：
    分析：根据相似多边形面积的比等于相似比的平方求出A1C，然后根据平移距离等于对应点A、A1的距离求解即可．
    解答：解：∵重叠部分的面积是正方形ABCD的面积的一半，
    ∴（
    A1C
    AC
    ）2=
    1
    2
    ，
    ∴A1C=
    		2
    2
    ×
    		2
    =1，
    ∴平移的距离=AC-A1C=
    		2
    -1．
    故答案为：
    		2
    -1．
    点评：本题考查了平移的性质，相似多边形的性质，熟记各性质并求出A1C的长度是解题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    三角形两边长分别为2和4，第三边是方程x2-6x+8=0的解，则这个三角形的周长是（　　）
    A、10B、8或10
    C、8D、8和10

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    ∠AOB如图所示，其中O、A、B是正方形网格上的三个格点．
    （1）利用格点画图：
    ①取线段OB的中点P，
    ②过点P画OA的垂线，垂足为H，
    ③过点P画OB的垂线，交OA于点C．
    （2）线段PH的长度是点P到直线
     
    的距离，线段
     
    是点O到直线PC的距离．
    （3）因为直线外一点到直线上各点连接的所有线中，垂线段最短，所以线段OP、PH、OC这三条线段大小关系是
     
    （用“＜”号连接）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    若（a+1）2+|b-2|=0，则2a+1008b=
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在梯形ABCD中，AD∥BC，将腰AB沿底BC平移至DE，若点E恰好是BC的中点，那么点F是DE的中点吗？写出你的结论，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    圣诞节来临，利华精品玩具店以每个60元的价格购进某种玩具，决定每个玩具不得低于80元出售．玩具的销售单价m（元/个）与每天的销售数量n（个）之间的函数关系如图所示．
    （1）试求表示线段AB的函数的解析式，并求出当销售数量n=20时单价m的值；
    （2）写出该店当每天销售n（30≥n≥10）个时，所获得利润w（元）与n（个）之间的函数关系式；
    （3）店长李明经过一段时间的销售发现，每天卖27个赚的钱反而比每天卖30个赚的钱多，如果不采用直接求值的方式，你能用所学的数学知识解释这一现象吗？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

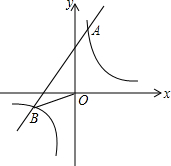    如图，已知反比例函数y1=
    k
    x
    与一次函数y2=ax+b的图象相交于两点A（1，3）B（n，-1）
    （1）分别求出反比例函数与一次函数的函数关系式；
    （2）观察图象，直接写出使得y1＞y2成立的自变量x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    某广告公司制作广告的收费标准是：以面积为单位，在不超过规定的面积A（m2）的范围内，每张广告费1000元，如果超过A（m2），则除了要交这1000元的基本广告费以外，超过的部分还要按每平方米50A元交费．下表是该公司对两家用户广告面积和收费情况的记载：
    单位广告的面积（m2）收费金额（元）
    烟草公司61400
    食品公司31000
    红星公司要制作一张大型公益广告，其材料形状是矩形，它的四周是空白，如图，如果上、下各空0.25m，左右各空0.5m，那么，空白部分的面积为6m2．已知矩形材料的长比宽多1m，并且空白部分不收广告费，中间的矩形部分才是广告面积，如果这张广告的广告费为2600元，那么四周的空白部分的面积是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    下列说法：
    ①在∠ABC的边BC的延长线上取一点D；
    ②线段AB与线段BA是同一条线段；
    ③若∠1+∠2+∠3=90°，则∠1、∠2、∠3互余；
    ④两点之间的线段，叫做两点之间的距离．
    其中正确的个数是（　　）
    A、1个B、2个C、3个D、4个

    查看答案和解析>>

    同步练习册答案