
【题目】如图,在四边形![]() 中,
中,![]() ,点E为AD边上一点,连接BD、CE,CE与BD交于点F,且CE∥AB,若
,点E为AD边上一点,连接BD、CE,CE与BD交于点F,且CE∥AB,若![]() ,则BC的长为__________.
,则BC的长为__________.

【答案】![]()
【解析】
连接AC交BD于点O,由题意可证AC垂直平分BD,△ABD是等边三角形,可得∠BAO=∠DAO=30°,AB=AD=BD=8,BO=OD=4,通过证明△EDF是等边三角形,可得DE=EF=DF=2,由勾股定理可求OC,BC的长.
如图,连接AC交BD于点O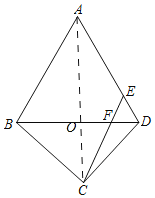
∵AB=AD,BC=DC,∠A=60°,
∴AC垂直平分BD,△ABD是等边三角形
∴∠BAO=∠DAO=30°,AB=AD=BD=8,
BO=OD=4
∵CE∥AB
∴∠BAO=∠ACE=30°,∠CED=∠BAD=60°
∴∠DAO=∠ACE=30°
∴AE=CE=6
∴DE=AD-AE=2
∵∠CED=∠ADB=60°
∴△EDF是等边三角形
∴DE=EF=DF=2
∴CF=CE-EF=4,OF=OD-DF=2
∴OC=![]() ,
,
∴BC=![]()


科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点![]() 若点D为BC边的中点,点M为线段EF上一动点,则
若点D为BC边的中点,点M为线段EF上一动点,则![]() 周长的最小值为
周长的最小值为![]()
![]()

A. 6 B. 8 C. 10 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的边长为8,AD是BC边上的中线,点E是AC边上的一点,AE=2,若点M是线段AD上的一个动点,则ME+MC的最小值为____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ABC=60°,AD、CE分别平分∠BAC、∠ACB,

(1)求∠AOC的度数
(2)连接BO,试说明BO平分∠ABC
(3)判断AC、AE、CD的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有A、B两个港口,水由A流向B,水流的速度是4千米/小时,甲、乙两船同时由A顺流驶向B,各自不停地在A、B之间往返航行,甲在静水中的速度是28千米/小时,乙在静水中的速度是20千米/小时.

设甲行驶的时间为t小时,甲船距B港口的距离为S1千米,乙船距B港口的距离为S2千米,如图为S1(千米)和t(小时)函数关系的部分图象.
(1)A、B两港口距离是_____千米.
(2)在图中画出乙船从出发到第一次返回A港口这段时间内,S2(千米)和t(小时)的函数关系的图象.
(3)求甲、乙两船第二次(不算开始时甲、乙在A处的那一次)相遇点M位于A、B港口的什么位置?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,A(0,4),B(﹣3,0),C(2,0),D为B点关于AC的对称点,反比例函数y=![]() 的图象经过D点.
的图象经过D点.

(1)证明四边形ABCD为菱形;
(2)求此反比例函数的解析式;
(3)已知在y=![]() 的图象(x>0)上一点N,y轴正半轴上一点M,且四边形ABMN是平行四边形,求M点的坐标.
的图象(x>0)上一点N,y轴正半轴上一点M,且四边形ABMN是平行四边形,求M点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,轮船从B处以每小时60海里的速度沿南偏东20°方向匀速航行,在B处观测灯塔A位于南偏东50°方向上,轮船航行20分钟到达C处,在C处观测灯塔A位于北偏东10°方向上,则C处与灯塔A的距离是___________海里.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,我市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:

(1)接受问卷调查的学生共有_______人,扇形统计图中“基本了解”部分所对应扇形的圆心角为_______°;
(2)请补全条形统计图;
(3)若该中学共有学生1800人,请根据上述调查结果,估计该中学学生中对校园安全知识 达到“了解”和“基本了解”程度的总人数;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,∠C=∠EDF=60°,AB=1,现将∠EDF绕点D任意旋转,分别交边AB、BC于点E、F(不与菱形的顶点重合),连接EF,则△BEF的周长最小值是_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com