练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    10．如图所示，已知点A，D，B，F在一条直线上，△ABC≌△FDE，∠A和∠F是对应角．求证：
    （1）AC∥EF；
    （2）AD=FB．

    分析 （1）根据全等三角形的性质得到∠A=∠F，根据平行线的性质证明；
    （2）根据全等三角形的性质得到AB=FD，结合图形证明即可．

    解答 证明：（1）∵△ABC≌△FDE，
    ∴∠A=∠F，
    ∴AC∥EF；
    （2）∵△ABC≌△FDE，
    ∴AB=FD，
    ∴AB-BD=FD-BD，即AD=FB．

    点评 本题考查的是全等三角形的性质，掌握全等三角形的对应边相等、全等三角形的对应角相等是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    20．（1）计算：$\root{3}{8}$+|2-$\sqrt{3}$|-20140-（$\frac{1}{2}$）-1
    （2）解方程：$\frac{x-2}{x+2}$-1=$\frac{8}{{{x^2}-4}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．若不等式组$\left\{\begin{array}{l}x-a＞1\\ b-3x＞0\end{array}\right.$的解集是-1＜x＜1，则a、b的值分别是-2，3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．解方程：
    （1）$\frac{3}{x+2}$+$\frac{1}{x}$=$\frac{4}{{{x^2}+2x}}$；                           
    （2）$\frac{x}{x+2}$-$\frac{x+2}{2-x}$=$\frac{8}{{{x^2}-4}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如果（x+$\frac{1}{x}$）2=$\frac{25}{4}$，试用配方法求（x-$\frac{1}{x}$）2的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．如图，在直角坐标系中，正方形ABCD的点B、C在轴上，已知抛物线y=x2过点A、点D，求点A，点D的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．已知5a=4b，求：
    （1）$\frac{a-b}{b}$；（2）$\frac{a+b}{b}$；（3）$\frac{a-b}{a+b}$．

    查看答案和解析>>

    科目：初中数学 来源：2017届广东省东莞市堂星晨学校九年级第一次模拟数学试卷（解析版） 题型：判断题

    某商店购进一批单价为20元的日用品，如果以单价30元销售，那么半个月内可以售出400件.根据销售经验，提高销售单价会导致销售量的减少，即销售单价每提高1元，销售量相应减少20件.问如何提高售价,才能在半个月内获得最大利润？

    查看答案和解析>>

    科目：初中数学 来源：2017届内蒙古呼伦贝尔市海拉尔区九年级5月中考模拟考试数学试卷（解析版） 题型：单选题

    已知二次函数y＝a(x－1)2－c的图象如图所示，则一次函数y＝ax＋c的大致图象可能是（ ）

    A. 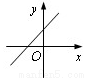B. C. D.

    查看答案和解析>>

    同步练习册答案