
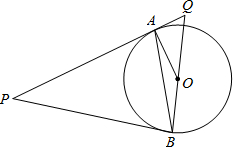
如图所示,P是⊙O外一点,PA是⊙O的切线,A是切点,B是⊙O 上一点,且PA=PB,连接AO、BO、AB,并延长BO与切线PA相交于点Q.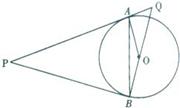
(1)求证:PB是⊙O的切线;
(2)求证:AQ•PQ=OQ•BQ;
(3)设∠AOQ=α,若cosα=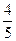 ,OQ=15,求AB的长.
,OQ=15,求AB的长.
[来源:学科网ZXXK]
解:(1)证明:连接OP,与AB交与点C.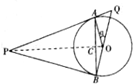
∵PA=PB,OA=OB,OP=OP,
∴△OAP≌△OBP(SSS ),
),
∴∠OBP=∠OAP,
∵PA是⊙O的切线,A是切点,
∴∠OAP=90°,
∴∠OBP=90°,即PB是⊙O的切线;
(2)∵ ∠Q=∠Q,∠OAQ=∠QBP=90°,
∠Q=∠Q,∠OAQ=∠QBP=90°,
∴△QAO∽△QBP,[来源:学+科+网Z+X+X+K]
∴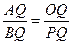 ,即AQ•PQ=OQ•BQ;
,即AQ•PQ=OQ•BQ;
(3)在Rt△OAQ中,∵OQ=15,cosα=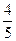 ,
,
∴OA=12,AQ=9,
∴QB=27;
∵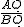 =
= 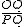 ,
,
∴PQ=45,即PA=36,
∴OP=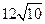 ;
;
∵PA、PB是⊙O的切线,
∴OP⊥AB,AC=BC,
∴PA•OA=OP•AC,即36×12=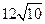 •AC,
•AC,
∴AC=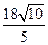 ,故AB=
,故AB=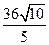 .
.
解析


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:
 =PB,连接AO、BO、AB,并延长BO与切线PA相交于点Q.
=PB,连接AO、BO、AB,并延长BO与切线PA相交于点Q.| 4 | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
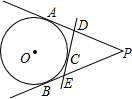 如图所示,P是⊙O外一点,PA,PB分别和⊙O切于A,B两点,C是
如图所示,P是⊙O外一点,PA,PB分别和⊙O切于A,B两点,C是 |
| AB |
| A、12 | B、6 | C、8 | D、4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
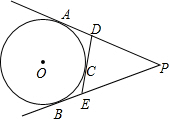 如图所示,P是⊙O外一点,PA,PB分别和⊙O切于A,B两点,C是
如图所示,P是⊙O外一点,PA,PB分别和⊙O切于A,B两点,C是 | AB |
查看答案和解析>>
科目:初中数学 来源:2011-2012学年浙江省翠苑中学九年级下学期3月考数学卷(带解析) 题型:解答题
如图所示.P是⊙O外一点.PA是⊙O的切线.A是切点.B是⊙O上一点.且PA=PB,连接AO、BO、AB,并延长BO与切线PA相交于点Q.
(1)求证:PB是⊙O的切线;
(2)求证: AQ?PQ= OQ?BQ;
(3)设∠AOQ=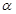 .若cos
.若cos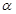 =
=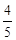 .OQ= 15.求AB的长
.OQ= 15.求AB的长
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com