
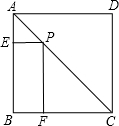
 如图,P为正方形ABCD的对角线AC上任意一点,PE⊥AB于E,PF⊥BC于F,若AC=$\sqrt{2}$,则四边形PEBF的周长为( )
如图,P为正方形ABCD的对角线AC上任意一点,PE⊥AB于E,PF⊥BC于F,若AC=$\sqrt{2}$,则四边形PEBF的周长为( )| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 2 | D. | 1 |
分析 首先根据正方形的性质和勾股定理可求出AB的长,再由条件可知:四边形PEBF为矩形,三角形AEP和三角形PFC为等腰直角三角形,所以PE+PF+BE+BF=2AB,问题得解.
解答 解:∵四边形ABCD是正方形,
∴∠A=90°,AB=BC,
∴AB2+BC2=AC2,
∵AC=$\sqrt{2}$,
∴AB=BC=1,
∵四边形ABCD是正方形,
∴∠BAC=∠BCA=45°,
∵PE⊥AB于E,PF⊥BC于F,
∴四边形PEBF为矩形,△AEP和△PFC为等腰直角三角形,
∴PF=BE,PE=AE,
∴PE+PF+BE+AE=2AB=2,
即四边形PEBF的周长为2,
故选C.
点评 本题考查了正方形的性质:①正方形的四条边都相等,四个角都是直角; ②正方形的两条对角线相等,互相垂直平分,并且每条对角线平分一组对角以及矩形的判断和矩形的性质,是一道不错的题目,解题的关键是利用勾股定理求出AB的长.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 160(1+a%)2=128 | B. | 160(1-a%)2=128 | C. | 160(1-2a%)=128 | D. | 160(1-a%)=128 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 一、二 | B. | 二、三 | C. | 三、四 | D. | 一、四 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC三个顶点都在5×5的网格(每个小正方形的边长均为1单位长度)的格点上,将△ABC绕点C顺时针旋转到△A′B′C的位置,且A′、B′仍落在格点上,求线段AC扫过的扇形所围成的圆锥体的底面半径.
如图,△ABC三个顶点都在5×5的网格(每个小正方形的边长均为1单位长度)的格点上,将△ABC绕点C顺时针旋转到△A′B′C的位置,且A′、B′仍落在格点上,求线段AC扫过的扇形所围成的圆锥体的底面半径.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=(x-2)2 | B. | y=-2(x+1)(x-1) | C. | y=1-x-x2 | D. | y=$\frac{1}{{x}^{2}-1}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com