
【题目】如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO.
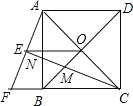
(1)已知BD=![]() ,求正方形ABCD的边长;
,求正方形ABCD的边长;
(2)猜想线段EM与CN的数量关系并加以证明.
【答案】(1)1;(2)CN=![]() CM,理由详见解析.
CM,理由详见解析.
【解析】
试题分析:(1)根据正方形的性质可得△ABD是等腰直角三角形,再由勾股定理可得2AB2=BD2,即可求得AB=1;(2)根据等腰三角形的性质可得CE⊥AF,再证得∠BAF=∠BCN,利用AAS证得△ABF≌△CBN,根据全等三角形的性质可得AF=CN,再证△ABF∽△COM,根据相似三角形的性质和正方形的性质即可证得CN=![]() CM.
CM.
试题解析:(1)∵四边形ABCD是正方形,
∴△ABD是等腰直角三角形,
∴2AB2=BD2,
∵BD=![]() ,
,
∴AB=1,
∴正方形ABCD的边长为1;
(2)CN=![]() CM.
CM.
证明:∵CF=CA,AF是∠ACF的平分线,
∴CE⊥AF,
∴∠AEN=∠CBN=90°,
∵∠ANE=∠CNB,
∴∠BAF=∠BCN,
在△ABF和△CBN中,
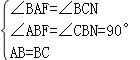 ,
,
∴△ABF≌△CBN(AAS),
∴AF=CN,
∵∠BAF=∠BCN,∠ACN=∠BCN,
∴∠BAF=∠OCM,
∵四边形ABCD是正方形,
∴AC⊥BD,
∴∠ABF=∠COM=90°,
∴△ABF∽△COM,
∴![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]() ,
,
即CN=![]() CM.
CM.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
【题目】(8分)在ΔABC中,AB=AC
(1)如图1,如果∠BAD=30°,AD是BC上的高,AD=AE,则∠EDC=__________
(2)如图2,如果∠BAD=40°,AD是BC上的高,AD=AE,则∠EDC=__________
(3)思考:通过以上两题,你发现∠BAD与∠EDC之间有什么关系?请用式子表示: _____________
(4)如图3,如果AD不是BC上的高,AD=AE,是否仍有上述关系?如有,请你写出来,并说明理由.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某农场有一块长40m,宽32m的矩形种植地,为方便管理,准备沿平行于两边的方向纵、横各修建一条等宽的小路,要使种植面积为1140m2,求小路的宽.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式中,计算过程正确的是( )
A. x3+x3=x3+3=x6
B. x3·x3=2x3
C. x·x3·x5=x0+3+5=x8
D. x2·(-x)3=-x2+3=-x5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP; ⑤∠AOB=60°.其中正确的结论的个数是( )

A.2个 B.3个 C. 4个 D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx+b的图像经过点(-1.-5),且与正比例函数y=![]() x的图象相交于点(2,m).
x的图象相交于点(2,m).
(1)求m的值;
(2)求一次函数y=kx+b的解析式;
(3)求这两个函数图像与x轴所围成的三角形面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com