
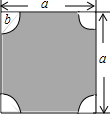
 如图,四个角是半径为b的$\frac{1}{4}$的圆形.请用图中的字母表示阴影部分的面积.
如图,四个角是半径为b的$\frac{1}{4}$的圆形.请用图中的字母表示阴影部分的面积. 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 测量员在测量一块地时,先从点A向北偏东30°走100m到点B,再从点B向北偏西60°走80m到点C,又从点C向南偏西30°走60m到点D,最后以最短的距离回到A,试回答下列问题
测量员在测量一块地时,先从点A向北偏东30°走100m到点B,再从点B向北偏西60°走80m到点C,又从点C向南偏西30°走60m到点D,最后以最短的距离回到A,试回答下列问题查看答案和解析>>
科目:初中数学 来源: 题型:解答题
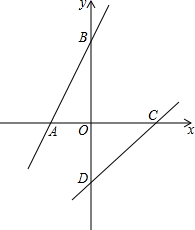 直线y=x+3分别交x轴、y轴于A、B两点,直线y=x-2分别交x轴、y 轴于C、D两点,在直线AB上是否存在一点P,使得S△PAD=S△PCD?若存在请求P点坐标,若不存在请说明理由.
直线y=x+3分别交x轴、y轴于A、B两点,直线y=x-2分别交x轴、y 轴于C、D两点,在直线AB上是否存在一点P,使得S△PAD=S△PCD?若存在请求P点坐标,若不存在请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,点M为抛物线y=-x2+2nx-n2+2n(n>2)的顶点,直线y=-$\frac{1}{2}$x与抛物线交于点P、Q,过点P作PA∥x轴,交抛物线于另一点A,交y轴于点B.
如图,在平面直角坐标系xOy中,点M为抛物线y=-x2+2nx-n2+2n(n>2)的顶点,直线y=-$\frac{1}{2}$x与抛物线交于点P、Q,过点P作PA∥x轴,交抛物线于另一点A,交y轴于点B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
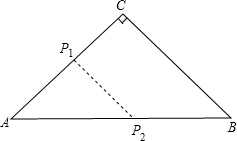 如图所示,△ABC为等腰直角三角形,P1,P2分别从A,B出发,速度都是1cm/s,P1运动到C为止,AB=100cm,t(s)后,S${\;}_{△A{P}_{1}{P}_{2}}$的面积与t(s)的函数关系为( )
如图所示,△ABC为等腰直角三角形,P1,P2分别从A,B出发,速度都是1cm/s,P1运动到C为止,AB=100cm,t(s)后,S${\;}_{△A{P}_{1}{P}_{2}}$的面积与t(s)的函数关系为( )| A. | S=t(100-t) | B. | S=$\frac{\sqrt{2}}{2}{t}^{2}-5\sqrt{2}t$ | C. | S=$\frac{\sqrt{2}}{2}{t}^{2}$ | D. | S=-$\frac{\sqrt{2}}{4}{t}^{2}+25\sqrt{2}t$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
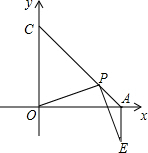 已知∠AC0=45°,P是线段AC上任一点,(P不与A、C重合),连OP,作PE⊥OP,且PE=OP,连AE,试判断AE和OA的位置关系,请说明理由.
已知∠AC0=45°,P是线段AC上任一点,(P不与A、C重合),连OP,作PE⊥OP,且PE=OP,连AE,试判断AE和OA的位置关系,请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com