
【题目】如图1,定义:在直角三角形ABC中,锐角α的邻边与对边的比叫做角α的余切,记作ctanα,即ctanα=![]() =
=![]() ,根据上述角的余切定义,解下列问题:
,根据上述角的余切定义,解下列问题:
(1)如图1,若BC=3,AB=5,则ctanB= ;
(2)ctan60°= ;
(3)如图2,已知:△ABC中,∠B是锐角,ctan C=2,AB=10,BC=20,试求∠B的余弦cosB的值.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)先利用勾股定理计算出AC=4,然后根据余切的定义求解;
(2)根据余切的定义得到ctan60°=![]() ,然后把tan60°=
,然后把tan60°=![]() 代入计算即可;
代入计算即可;
(3)作AH⊥BC于H,如图2,先在Rt△ACH中利用余切的定义得到ctanC=![]() =2,则可设AH=x,CH=2x,BH=BC﹣CH=20﹣2x,接着再在Rt△ABH中利用勾股定理得到(20﹣2x)2+x2=102,解得x1=6,x2=10(舍去),所以BH=8,然后根据余弦的定义求解.
=2,则可设AH=x,CH=2x,BH=BC﹣CH=20﹣2x,接着再在Rt△ABH中利用勾股定理得到(20﹣2x)2+x2=102,解得x1=6,x2=10(舍去),所以BH=8,然后根据余弦的定义求解.
解:(1)∵BC=3,AB=5,
∴AC=![]() =4,
=4,
∴ctanB=![]() =
=![]() ;
;
(2)ctan60°=![]() =
=![]() =
=![]() ;
;
(3)作AH⊥BC于H,如图2,
在Rt△ACH中,ctanC=![]() =2,
=2,
设AH=x,则CH=2x,
∴BH=BC﹣CH=20﹣2x,
在Rt△ABH中,∵BH2+AH2=AB2,
∴(20﹣2x)2+x2=102,解得x1=6,x2=10(舍去),
∴BH=20﹣2×6=8,
∴cosB=![]() =
=![]() =
=![]() .
.



科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AE是∠BAC的平分线,∠ABC的平分线 BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交AB于点F.
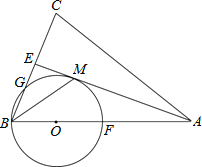
(1)求证:AE为⊙O的切线.
(2)当BC=8,AC=12时,求⊙O的半径.
(3)在(2)的条件下,求线段BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在方格纸内将△ABC水平向右平移4个单位得到△A′B′C′.
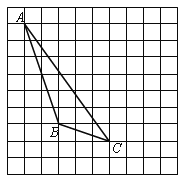
(1)补全△A′B′C′,利用网格点和直尺画图;
(2)图中AC与A1C1的关系是: ;
(3)画出AB边上的高线CD;
(4)画出△ABC中AB边上的中线CE;
(5)△BCE的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人同时开始采摘樱桃,甲平均每小时采摘8公斤樱桃,乙平均每小时采摘7公斤樱桃。采摘同时结束后,甲从他采摘的樱桃中取出1公斤给了乙,这时两人的樱桃一样多。他们采摘樱桃用了多长时间?设他们采摘了x小时,则下面所列方程中正确的是( )
A. 8x-1=7x+1 B. 8x-1=7x C. 8x+l=7x D. 8x+l=7x-1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F.将△DEF沿EF折叠,点D恰好落在BE上M点处,延长BC、EF交于点N, 有下列四个结论:
① DF=CF;②BF⊥EN;③△BEN是等边三角形;④S△BEF=3S△DEF. 其中,正确的结论有( )
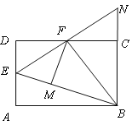
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com