
【题目】如图,△ABC内接于⊙O,AB=AC,CO的延长线交AB于点D
(1)求证:AO平分∠BAC;
(2)若BC=6,sin∠BAC= ![]() ,求AC和CD的长.
,求AC和CD的长.
【答案】
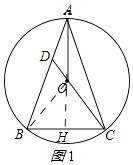
(1)证明:延长AO交BC于H,连接BO,如图1所示:
∵AB=AC,OB=OC,
∴A、O在线段BC的垂直平分线上,
∴AO⊥BC,
又∵AB=AC,
∴AO平分∠BAC;
(2)解:延长CD交⊙O于E,连接BE,如图2所示:
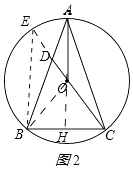
则CE是⊙O的直径,
∴∠EBC=90°,BC⊥BE,
∵∠E=∠BAC,
∴sinE=sin∠BAC,
∴ ![]() =
= ![]() ,
,
∴CE= ![]() BC=10,
BC=10,
∴BE= ![]() =8,OA=OE=
=8,OA=OE= ![]() CE=5,
CE=5,
∵AH⊥BC,
∴BE∥OA,
∴ ![]() ,即
,即 ![]() =
= ![]() ,
,
解得:OD= ![]() ,
,
∴CD=5+ ![]() =
= ![]() ,
,
∵BE∥OA,即BE∥OH,OC=OE,
∴OH是△CEB的中位线,
∴OH= ![]() BE=4,CH=
BE=4,CH= ![]() BC=3,
BC=3,
∴AH=5+4=9,
在Rt△ACH中,AC= ![]() =
= ![]() =3
=3 ![]() .
.
【解析】(1)圆中常用辅助线是连半径,利用垂直平分线的判定定理可得A、O均在线段BC的垂直平分线上,又由等腰三角形的性质“顶角平分线与高重合”得证;(2)出现三角函数时通常把它放在直角三角形中,因此需延长CD,构造出直径,进而构造出90度的圆周角即直角三角形,可求出直径CE、BE,由BE∥OA可求OD、CD,进而求出AH,利用勾股定理求出AC.
【考点精析】关于本题考查的三角形的外接圆与外心和解直角三角形,需要了解过三角形的三个顶点的圆叫做三角形的外接圆,其圆心叫做三角形的外心;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)才能得出正确答案.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示.A(2,3),B(3,1),C(﹣2,﹣2)三点在格点上.

(1)作出△ABC关于y轴对称的△A1B1C1;
(2)直接写出△ABC关于x轴对称的△A2B2C2的各点坐标;
(3)求出△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,l1表示某公司一种产品一天的销售收入与销售量的关系,l2表示该公司这种产品一天的销售成本与销售量的关系.
(1)x=1时,销售收入= 万元,销售成本= 万元,盈利(收入﹣成本)= 万元;
(2)一天销售 件时,销售收入等于销售成本;
(3)l2对应的函数表达式是 ;
(4)你能写出利润与销售量间的函数表达式吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB、BC、AC三边的长分别是![]() ,
,![]() ,
,![]() .
.
(1)△ABC的面积是 ;
(2)请在图1中作出△ABC关于直线l对称的△A1B1C1;
(3)请在图2中画出△DEF,是DE、EF、DF三边的长分别是![]() ,
,![]() ,
,![]() ,并判断△DEF的形状,说明理由.
,并判断△DEF的形状,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知BC=EC,∠BCE=∠ACD,如果只添加一个条件,使△ABC ≌ △DEC,则添加的条件不能为( )
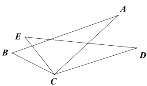
A. ∠B=∠E B. AC=DC C. ∠A=∠D D. AB=DE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下面不能判断是平行四边形的是( )

A. ∠B=∠D,∠BAD=∠BCD
B. AB∥CD,AD=BC
C. ∠B+∠DAB=180°,∠B+∠BCD=180°
D. AB∥CD,AB=CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算:(![]() ﹣
﹣![]() )2+(2
)2+(2![]() +
+![]() )(2
)(2![]() ﹣
﹣![]() )
)
(2)因式分解:9a2(x﹣y)+4b2(y﹣x)
(3)先化简,再求值:![]() ÷(a﹣1﹣
÷(a﹣1﹣![]() ),其中a2﹣a﹣6=0.
),其中a2﹣a﹣6=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】鄂州某个体商户购进某种电子产品的进价是50元/个,根据市场调研发现售价是80元/个时,每周可卖出160个,若销售单价每个降低2元,则每周可多卖出20个.设销售价格每个降低x元(x为偶数),每周销售量为y个.
(1)直接写出销售量y个与降价x元之间的函数关系式;
(2)设商户每周获得的利润为W元,当销售单价定为多少元时,每周销售利润最大,最大利润是多少元?
(3)若商户计划下周利润不低于5200元的情况下,他至少要准备多少元进货成本?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com