
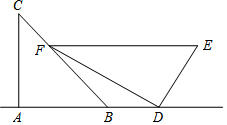
 小华是一位善于思考的学生,在一次数学活动课上,他将一副直角三角板如图位置摆放,A、B、D在同一直线上,EF∥AD,∠CAB=∠EDF=90°,∠C=45°,∠E=60°,量得DE=2$\sqrt{3}$.
小华是一位善于思考的学生,在一次数学活动课上,他将一副直角三角板如图位置摆放,A、B、D在同一直线上,EF∥AD,∠CAB=∠EDF=90°,∠C=45°,∠E=60°,量得DE=2$\sqrt{3}$.分析 (1)根据平行线的性质求出∠EFB,计算即可;
(2)根据直角三角形的性质求出DF,根据勾股定理求出FH、DH,计算即可.
解答 解:(1)∵EF∥AD,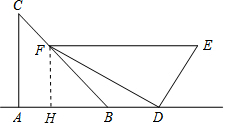
∴∠EFB=∠ABC=45°,
∴∠BFD=∠BFE-∠EFD=15°;
(2)作FH⊥AB于H,
∵∠E=60°,DE=2$\sqrt{3}$,
∴DF=6,
∵∠HDF=30°,
∴FH=$\frac{1}{2}$DF=3,
由勾股定理得,HD=$\sqrt{D{F}^{2}-F{H}^{2}}$=3$\sqrt{3}$,
∵∠ABC=45°,
∴HB=HF=3,
∴BD=HD-HB=3$\sqrt{3}$-3.
点评 本题考查的是勾股定理的应用,掌握如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
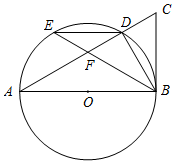 如图,AB为⊙O的直径,点D,E为⊙O上的两个点,延长AD至C,使∠CBD=∠BED.
如图,AB为⊙O的直径,点D,E为⊙O上的两个点,延长AD至C,使∠CBD=∠BED.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
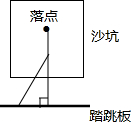 如图,体育课上老师测量跳远成绩是这样操作的:用一块直角三角板的一边附在踏跳板上,另一边与拉直的皮尺重合,并且使皮尺经过被测试同学的落点,这样做的理由是垂线段最短.
如图,体育课上老师测量跳远成绩是这样操作的:用一块直角三角板的一边附在踏跳板上,另一边与拉直的皮尺重合,并且使皮尺经过被测试同学的落点,这样做的理由是垂线段最短.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
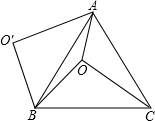 如图,O是等边△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,则∠AOB=150°.
如图,O是等边△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,则∠AOB=150°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com