
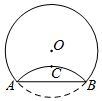
 如图,将半径为3cm的圆形纸片折叠后,劣弧中点C恰好与圆心O距离1cm,则折痕AB的长为2$\sqrt{5}$cm.
如图,将半径为3cm的圆形纸片折叠后,劣弧中点C恰好与圆心O距离1cm,则折痕AB的长为2$\sqrt{5}$cm. 科目:初中数学 来源: 题型:解答题
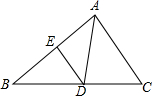 如图,△ABC中,D是BC上一点,∠DAC=∠B,E为AB上一点.
如图,△ABC中,D是BC上一点,∠DAC=∠B,E为AB上一点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
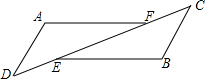 如图△ADF和△BCE中,∠A=∠B,点D、E、F、C在同一直线上,有如下三个关系式:①AD=BC;②DE=CF;③BE∥AF.
如图△ADF和△BCE中,∠A=∠B,点D、E、F、C在同一直线上,有如下三个关系式:①AD=BC;②DE=CF;③BE∥AF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{\sqrt{5}}{5}$ | C. | $\sqrt{5}$ | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明从家去体育场锻炼,同时,妈妈从体育场以50米/分的速度回家,小明到体育场后发现要下雨,立即返回,追上妈妈后,小明以250米/分的速度回家取伞,立即又以250米/分的速度折回接妈妈,并一同回家.如图是两人离家的距离y(米)与小明出发的时间x(分)之间的函数图象.
小明从家去体育场锻炼,同时,妈妈从体育场以50米/分的速度回家,小明到体育场后发现要下雨,立即返回,追上妈妈后,小明以250米/分的速度回家取伞,立即又以250米/分的速度折回接妈妈,并一同回家.如图是两人离家的距离y(米)与小明出发的时间x(分)之间的函数图象.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  ∵$\widehat{AD}$=$\widehat{BC}$ ∴AB=CD | B. | 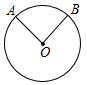 ∵$\widehat{AB}$的度数为40° ∴∠AOB=80° | ||
| C. | 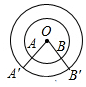 ∵∠AOB=∠A′OB′ ∴$\widehat{AB}$=$\widehat{A′B′}$ | D. | 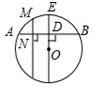 ∵MN垂直平分AD ∴$\widehat{MA}$=$\widehat{ME}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com