
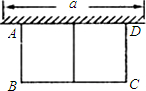
 如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度a为10m)围成中间隔有一道篱笆的长方形花辅,设花圃的宽AB为x(m),面积为y(m2),求:
如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度a为10m)围成中间隔有一道篱笆的长方形花辅,设花圃的宽AB为x(m),面积为y(m2),求:科目:初中数学 来源: 题型:
 20、如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度a为10m)围成中间隔有一道篱笆的长方形花圃,设花圃的宽AB为xm,面积为Sm.
20、如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度a为10m)围成中间隔有一道篱笆的长方形花圃,设花圃的宽AB为xm,面积为Sm.查看答案和解析>>
科目:初中数学 来源: 题型:
 长方形养鸡场.设养鸡场的长BC为xm,面积为ym2.
长方形养鸡场.设养鸡场的长BC为xm,面积为ym2.查看答案和解析>>
科目:初中数学 来源:2013届安徽省定远中学九年级第一次素质考试数学试卷(带解析) 题型:解答题
如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度a为10m),围成中间隔有一道篱笆的长方形花圃.设花圃的宽AB为xm,面积为Sm2.
(1)求S与x的函数关系式;
(2)如果要围成面积为45m2的花圃,AB的长是多少米?
(3)能围成面积比45 m2更大的花圃吗?如果能,请求出最大面积,并说明围法;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2012-2013学年安徽省九年级第一次素质考试数学试卷(解析版) 题型:解答题
如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度a为10m),围成中间隔有一道篱笆的长方形花圃.设花圃的宽AB为xm,面积为Sm2.
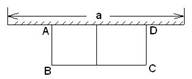
(1)求S与x的函数关系式;
(2)如果要围成面积为45m2的花圃,AB的长是多少米?
(3)能围成面积比45 m2更大的花圃吗?如果能,请求出最大面积,并说明围法;如果不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com