
【题目】如图1,抛物线C:y=x2经过变化可得到抛物线C1:y1=a1x(x﹣b1),C1与x轴的正半轴交与点A1,且其对称轴分别交抛物线C,C1于点B1,D1,此时四边形OB1A1D1恰为正方形;按上述类似方法,如图2,抛物线C1:y1=a1x(x﹣b1)经过变换可得到抛物线C2:y2=a2x(x﹣b2),C2与x轴的正半轴交与点A2,且其对称轴分别交抛物线C1,C2于点B2,D2,此时四边形OB2A2D2也恰为正方形;按上述类似方法,如图3,可得到抛物线C3:y3=a3x(x﹣b3)与正方形OB3A3D3.请探究以下问题:
(1)填空:a1= ,b1= ;
(2)求出C2与C3的解析式;
(3)按上述类似方法,可得到抛物线Cn:yn=anx(x﹣bn)与正方形OBnAnDn(n≥1).
①请用含n的代数式直接表示出Cn的解析式;
②当x取任意不为0的实数时,试比较y2015与y2016的函数值的大小并说明理由.

【答案】(1)、1,2;(2)、y2=x(x﹣6);y3=x(x﹣14);(3)、yn=x2﹣(2n+1﹣2)x;当x<0时,y2015<y2016;当x>0时,y2015>y2016.
【解析】
试题分析:(1)、根据图形变换后二次项系数不变得出a1=1,代入抛物线C1解析式后,求与x轴交点A1坐标,根据正方形对角线性质表示出B1的坐标,代入对应的解析式即可求出对应的b1的值;(2)、根据图形变换后二次项系数不变得出a2=a1=1,代入抛物线C2解析式后,求与x轴交点A2坐标,根据正方形对角线性质表示出B2的坐标,代入对应的解析式即可求出对应的b2的值,写出抛物线C2的解析式;再利用相同的方法求抛物线C3的解析式;(3)、①根据图形变换后二次项系数不变得出an=a1=1,由B1坐标(1,1)、B2坐标(3,3)、B3坐标(7,7)得Bn坐标(2n﹣1,2n﹣1),则bn=2(2n﹣1)=2n+1﹣2(n≥1),写出抛物线Cn解析式.
②先求抛物线C2015和抛物线C2016的交点为(0,0),在交点的两侧观察图形得出y2015与y2016的函数值的大小.
试题解析:(1)、由抛物线C经过变换得到抛物线C1,则a1=1, 代入C1得:y1=x(x﹣b1),
y1=0时,x(x﹣b1)=0 x1=0,x2=b1 ∴A1(b1,0)
由正方形OB1A1D1得:OA1=B1D1=b1 ∴B1(![]() ,
,![]() )
)
∵B1在抛物线c上,则![]() =
=![]() b1(b1﹣2)=0 b1=0(不符合题意),b1=2
b1(b1﹣2)=0 b1=0(不符合题意),b1=2
(2)、由a2=a1=1得,y2=x(x﹣b2), y2=0时,x(x﹣b2)=0 x1=0,x2=b2 ∴A2(b2,0)
由正方形OB2A2D2得:OA2=B2D2=b2 ∴B2(![]() ,
,![]() ) ∵B2在抛物线c1上,则
) ∵B2在抛物线c1上,则![]() =(
=(![]() )2﹣2×
)2﹣2×![]() ,
,
b2(b2﹣6)=0 b2=0(不符合题意),b2=6 ∴C2的解析式:y2=x(x﹣6)=x2﹣6x,
由a3=a2=1得,y3=x(x﹣b3), y3=0时,x(x﹣b3)=0 x1=0,x2=b3 ∴A3(b3,0)
由正方形OB3A3D3得:OA3=B3D3=b3 ∴B3(![]() ,
,![]() ) ∵B3在抛物线c2上,则
) ∵B3在抛物线c2上,则![]() =(
=(![]() )2﹣6×
)2﹣6×![]() ,
,
b3(b3﹣14)=0 b3=0(不符合题意),b3=14 ∴C3的解析式:y3=x(x﹣14)=x2﹣14x,
(3)、①Cn的解析式:yn=x2﹣(2n+1﹣2)x(n≥1).
②由上题可得抛物线C2015的解析式为:y2015=x2﹣x=x2﹣x
抛物线C2016的解析式为:y2016=x2﹣x=x2﹣x
∴两抛物线的交点为(0,0);
∴当x<0时,y2015<y2016;当x>0时,y2015>y2016.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
【题目】点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a﹣b|.利用数形结合思想回答下列问题:
(1)数轴上表示2和5的两点之间的距离是 , 数轴上表示2和﹣3的两点之间的距离是
(2)数轴上表示x和﹣2的两点之间的距离表示为 .
(3)若x表示一个有理数,且﹣4≤x≤﹣2,则|x﹣2|+|x+4|=
(4)若|x+3|+|x﹣5|=8,利用数轴求出x的整数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校就“遇见老人摔倒后如何处理”的问题,随机抽取该校部分学生进行问卷调查(每个被调查的学生必须选择而且只能在4种方式中选择一项),图1和图2是整理数据后绘制的两幅不完整的统计图,请根据图中提供的信息,解答下列问题: 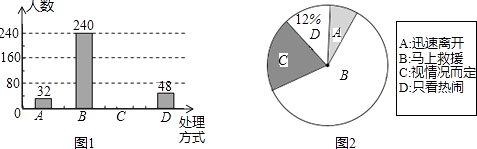
(1)该校随机抽查了名学生;
(2)将图1补充完整,在图2中,“视情况而定”部分所占的圆心角是度;
(3)估计该校2800名学生中采取“马上救助”的方式的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应南充市创建“全国卫生城市”的号召,某校1500名学生参加了卫生知识竞赛,成绩记为A、B、C、D四等.从中随机抽取了部分学生成绩进行统计,绘制成如图两幅不完整的统计图表,根据图表信息,以下说法不正确的是( ) 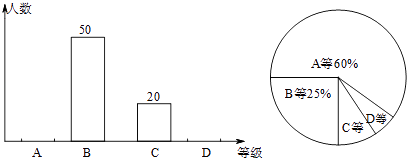
A.样本容量是200
B.D等所在扇形的圆心角为15°
C.样本中C等所占百分比是10%
D.估计全校学生成绩为A等大约有900人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,与x轴的一个交点在(﹣3,0)和(﹣2,0)之间,其部分图象如图所示,则下列结论中不正确的是( )
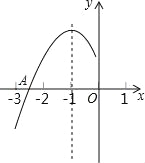
A.4ac﹣b2<0
B.2a﹣b=0
C.a+b+c<0
D.点(x1,y1)、(x2,y2)在抛物线上,若x1<x2,则y1<y2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知射线AB与直线CD交于点O,OF平分∠BOC,OG⊥OF于O,AE∥OF,且∠A=30°. 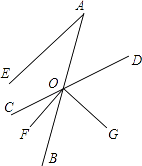
(1)求∠DOF的度数;
(2)试说明OD平分∠AOG.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com