
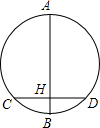
 如图所示圆中,AB为直径,弦CD⊥AB,垂足为H.若HB=2,HD=4,则AH=8.
如图所示圆中,AB为直径,弦CD⊥AB,垂足为H.若HB=2,HD=4,则AH=8.  名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
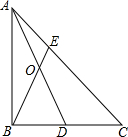 如图,在△ABC中,D为BC边的中点,E为AC边上的任意一点,BE交AD于点0.
如图,在△ABC中,D为BC边的中点,E为AC边上的任意一点,BE交AD于点0.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
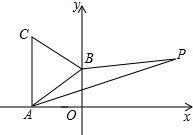 如图所示,A(-$\sqrt{3}$,0)、B(0,1)分别为x轴、y轴上的点,△ABC为等边三角形,点P(3,a)在第一象限内,且满足2S△ABP=S△ABC,求a的值.
如图所示,A(-$\sqrt{3}$,0)、B(0,1)分别为x轴、y轴上的点,△ABC为等边三角形,点P(3,a)在第一象限内,且满足2S△ABP=S△ABC,求a的值.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
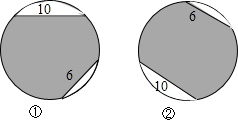 在图①、图②中的两个等圆中,各有两条长分别为10和6的弦,两图阴影面积S的大小关系为( )
在图①、图②中的两个等圆中,各有两条长分别为10和6的弦,两图阴影面积S的大小关系为( )| A. | S①>S② | B. | S①<S② | C. | S①=S② | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
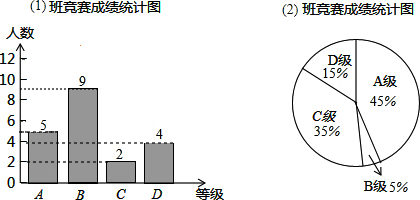
| 平均数(分) | 中位数(分) | 众数(分) | |
| 1班 | 87.5 | 90 | ②90 |
| 2班 | 88 | ①85 | 100 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,学校课外生物小组的试验园地是边长为20米的正方形,为了便于管理,现要在中间开辟一横一纵共两条等宽的小道,要使种植面积为361平方米,求小道的宽.
如图,学校课外生物小组的试验园地是边长为20米的正方形,为了便于管理,现要在中间开辟一横一纵共两条等宽的小道,要使种植面积为361平方米,求小道的宽.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com