
ΓΨΧβΡΩΓΩ»γΆΦ1Θ§≈ΉΈοœΏy=ax2+2x+c”κx÷αΫΜ”ΎAΘ®©¹4Θ§0Θ©Θ§BΘ®1Θ§0Θ©ΝΫΒψΘ§ΙΐΒψBΒΡ÷±œΏy=kx+![]() Ζ÷±π”κy÷αΦΑ≈ΉΈοœΏΫΜ”ΎΒψCΘ§DΘ°
Ζ÷±π”κy÷αΦΑ≈ΉΈοœΏΫΜ”ΎΒψCΘ§DΘ°
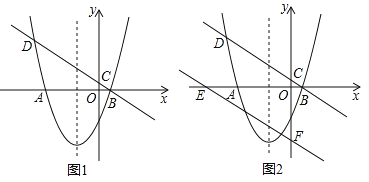
Θ®1Θ©«σ÷±œΏΚΆ≈ΉΈοœΏΒΡ±μ¥ο ΫΘΜ
Θ®2Θ©Ε·ΒψP¥”ΒψO≥ωΖΔΘ§‘Ύx÷αΒΡΗΚΑκ÷α…œ“‘ΟΩΟκ1ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»œρΉσ‘»ΥΌ‘ΥΕ·Θ§…η‘ΥΕ· ±ΦδΈΣtΟκΘ§Β±tΈΣΚΈ÷Β ±Θ§ΓςPDCΈΣ÷±Ϋ«»ΐΫ«–ΈΘΩ«κ÷±Ϋ”–¥≥ωΥυ”–¬ζΉψΧθΦΰΒΡtΒΡ÷ΒΘΜ
Θ®3Θ©»γΆΦ2Θ§ΫΪ÷±œΏBD―Ίy÷αœρœ¬ΤΫ“Τ4ΗωΒΞΈΜΚσΘ§”κx÷αΘ§y÷αΖ÷±πΫΜ”ΎEΘ§FΝΫΒψΘ§‘Ύ≈ΉΈοœΏΒΡΕ‘≥Τ÷α…œ «Ζώ¥φ‘ΎΒψMΘ§‘Ύ÷±œΏEF…œ «Ζώ¥φ‘ΎΒψNΘ§ ΙDM+MNΒΡ÷ΒΉν–ΓΘΩ»τ¥φ‘ΎΘ§«σ≥ωΤδΉν–Γ÷ΒΦΑΒψMΘ§NΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©≈ΉΈοœΏΫβΈω ΫΈΣΘΚy=![]() Θ§BDΫβΈω ΫΈΣy=©¹
Θ§BDΫβΈω ΫΈΣy=©¹![]() ΘΜΘ®2Θ©tΒΡ÷ΒΈΣ
ΘΜΘ®2Θ©tΒΡ÷ΒΈΣ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() Θ°Θ®3Θ©NΒψΉχ±ξΈΣΘ®©¹2Θ§©¹2Θ©Θ§MΒψΉχ±ξΈΣΘ®©¹
Θ°Θ®3Θ©NΒψΉχ±ξΈΣΘ®©¹2Θ§©¹2Θ©Θ§MΒψΉχ±ξΈΣΘ®©¹![]() Θ§©¹
Θ§©¹![]() Θ©Θ§
Θ©Θ§![]() .
.
ΓΨΫβΈωΓΩΘ®1Θ©άϊ”Ο¥ΐΕ®œΒ ΐΖ®«σΫβΩ…ΒΟΘΜ
Θ®2Θ©œ»«σΒΟΒψDΒΡΉχ±ξΘ§ΙΐΒψDΖ÷±πΉςDEΓΆx÷αΓΔDFΓΆy÷αΘ§Ζ÷P1DΓΆP1CΓΔP2DΓΆDCΓΔP3CΓΆDC»ΐ÷÷«ιΩωΘ§άϊ”ΟœύΥΤ»ΐΫ«–ΈΒΡ–‘÷ ÷π“Μ«σΫβΩ…ΒΟΘΜ
Θ®3Θ©Ά®ΙΐΉςΕ‘≥ΤΒψΘ§ΫΪ’έœΏΉΣΜ·≥…ΝΫΒψΦδΨύάκΘ§”Π”ΟΝΫΒψ÷°ΦδœΏΕΈΉνΕΧΘ°
Θ®1Θ©Α―AΘ®©¹4Θ§0Θ©Θ§BΘ®1Θ§0Θ©¥ζ»κy=ax2+2x+cΘ§
ΒΟ![]() Θ§
Θ§
ΫβΒΟΘΚ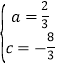 Θ§
Θ§
Γύ≈ΉΈοœΏΫβΈω ΫΈΣΘΚy=![]() Θ§
Θ§
ΓΏΙΐΒψBΒΡ÷±œΏy=kx+![]() Θ§
Θ§
Γύ¥ζ»κΘ®1Θ§0Θ©Θ§ΒΟΘΚk=©¹![]() Θ§
Θ§
ΓύBDΫβΈω ΫΈΣy=©¹![]() ΘΜ
ΘΜ
Θ®2Θ©”…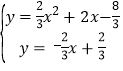 ΒΟΫΜΒψΉχ±ξΈΣDΘ®©¹5Θ§4Θ©Θ§
ΒΟΫΜΒψΉχ±ξΈΣDΘ®©¹5Θ§4Θ©Θ§
»γΆΦ1Θ§ΙΐDΉςDEΓΆx÷α”ΎΒψEΘ§ΉςDFΓΆy÷α”ΎΒψFΘ§
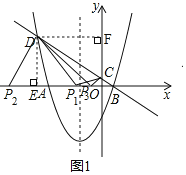
Β±P1DΓΆP1C ±Θ§ΓςP1DCΈΣ÷±Ϋ«»ΐΫ«–ΈΘ§
‘ρΓςDEP1ΓΉΓςP1OCΘ§
Γύ![]() =
=![]() Θ§Φ¥
Θ§Φ¥![]() =
=![]() Θ§
Θ§
ΫβΒΟt=![]() Θ§
Θ§
Β±P2DΓΆDC”ΎΒψD ±Θ§ΓςP2DCΈΣ÷±Ϋ«»ΐΫ«–Έ
”…ΓςP2DBΓΉΓςDEBΒΟ![]() =
=![]() Θ§
Θ§
Φ¥![]() =
=![]() Θ§
Θ§
ΫβΒΟΘΚt=![]() ΘΜ
ΘΜ
Β±P3CΓΆDC ±Θ§ΓςDFCΓΉΓςCOP3Θ§
Γύ![]() =
=![]() Θ§Φ¥
Θ§Φ¥![]() =
=![]() Θ§
Θ§
ΫβΒΟΘΚt=![]() Θ§
Θ§
ΓύtΒΡ÷ΒΈΣ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() Θ°
Θ°
Θ®3Θ©”…“―÷Σ÷±œΏEFΫβΈω ΫΈΣΘΚy=©¹![]() x©¹
x©¹![]() Θ§
Θ§
‘Ύ≈ΉΈοœΏ…œ»ΓΒψDΒΡΕ‘≥ΤΒψDΓδΘ§ΙΐΒψDΓδΉςDΓδNΓΆEF”ΎΒψNΘ§ΫΜ≈ΉΈοœΏΕ‘≥Τ÷α”ΎΒψM
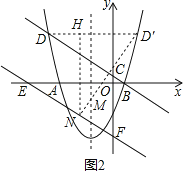
ΙΐΒψNΉςNHΓΆDDΓδ”ΎΒψHΘ§¥Υ ±Θ§DM+MN=DΓδNΉν–ΓΘ°
‘ρΓςEOFΓΉΓςNHDΓδ
…ηΒψNΉχ±ξΈΣΘ®aΘ§©¹![]() Θ©Θ§
Θ©Θ§
Γύ![]() =
=![]() Θ§Φ¥
Θ§Φ¥![]() =
=![]() Θ§
Θ§
ΫβΒΟΘΚa=©¹2Θ§
‘ρNΒψΉχ±ξΈΣΘ®©¹2Θ§©¹2Θ©Θ§
«σΒΟ÷±œΏNDΓδΒΡΫβΈω ΫΈΣy=![]() x+1Θ§
x+1Θ§
Β±x=©¹![]() ±Θ§y=©¹
±Θ§y=©¹![]() Θ§
Θ§
ΓύMΒψΉχ±ξΈΣΘ®©¹![]() Θ§©¹
Θ§©¹![]() Θ©Θ§
Θ©Θ§
¥Υ ±Θ§DM+MNΒΡ÷ΒΉν–ΓΈΣ![]() =
=![]() =2
=2![]() Θ°
Θ°


 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΫ®…η÷–ΒΡ¥σΆβΜΖ¬Ζ «Έ“ –ΒΡ“Μœν÷ΊΒψΟώ…ζΙΛ≥Χ.Ρ≥ΙΛ≥ΧΙΪΥΨ≥–Ϋ®ΒΡ“ΜΕΈ¬ΖΜυΙΛ≥ΧΒΡ ©ΙΛΆΝΖΫΝΩΈΣ120ΆρΝΔΖΫΘ§‘≠ΦΤΜ°”…ΙΪΥΨΒΡΦΉΓΔ““ΝΫΗωΙΛ≥ΧΕ”¥”ΙΪ¬ΖΒΡΝΫΕΥΆ§ ±œύœρ ©ΙΛ150ΧλΆξ≥….”…”ΎΧΊ β«ιΩω–η“ΣΘ§ΙΪΥΨ≥ιΒςΦΉΕ”Άβ‘° ©ΙΛΘ§”…““Ε”œ»ΒΞΕά ©ΙΛ40ΧλΚσΦΉΕ”ΖΒΜΊΘ§ΝΫΕ””÷Ι≤Ά§ ©ΙΛΝΥ110ΧλΘ§’β ±ΦΉ““ΝΫΕ”Ι≤Άξ≥…ΆΝΖΫΝΩ103.2ΆρΝΔΖΫ.
Θ®1Θ©Έ ΦΉΓΔ““ΝΫΕ”‘≠ΦΤΜ°ΤΫΨυΟΩΧλΒΡ ©ΙΛΆΝΖΫΝΩΖ÷±πΈΣΕύ…ΌΆρΝΔΖΫΘΩ
Θ®2Θ©‘Ύ≥ιΒςΦΉΕ”Άβ‘° ©ΙΛΒΡ«ιΩωœ¬Θ§ΈΣΝΥ±Θ÷Λ150ΧλΆξ≥…»ΈΈώΘ§ΙΪΥΨΈΣ““Ε”–¬ΙΚΫχΝΥ“Μ≈ζΜζ–Βά¥ΧαΗΏ–߬ Θ§Ρ«Ο¥““Ε”ΤΫΨυΟΩΧλΒΡ ©ΙΛΆΝΖΫΝΩ÷Ν…Ό“Σ±»‘≠ά¥ΧαΗΏΕύ…ΌΆρΝΔΖΫ≤≈Ρή±Θ÷ΛΑ¥ ±Άξ≥…»ΈΈώΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣΗέΩΎAΕΪΤΪΡœ10ΓψΖΫœρ”–“Μ¥Π–ΓΒΚBΘ§“ΜΥ“Μθ¬÷¥”ΗέΩΎA―ΊΡœΤΪΕΪ40ΓψΚΫœΏ≥ωΖΔΘ§–– Μ80ΚΘάοΒΫ¥οC¥ΠΘ§¥Υ ±Ιέ≤β–ΓΒΚB‘Ύ±±ΤΪΕΪ60ΓψΖΫœρΘ°
Θ®1Θ©«σ¥Υ ±Μθ¬÷ΒΫ–ΓΒΚBΒΡΨύάκΘ°
Θ®2Θ©‘Ύ–ΓΒΚ÷ήΈß36ΚΘάοΖΕΈßΡΎ «ΑΒΫΗ«χΘ§¥Υ ±¬÷¥§œρ’ΐΕΪΖΫœρΚΫ––”–ΟΜ”–¥ΞΫΗΈΘœ’ΘΩ«κΉς≥ω≈–Εœ≤ΔΥΒΟςάμ”…Θ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ ΆΤάμΧνΩ’
“―÷ΣΘΚ»γΆΦΥυ ΨΘ§ΒψBΘ§CΘ§E‘ΎΆ§“ΜΧθ÷±œΏ…œΘ§ABΓΈCDΘ§Γœ1=Γœ2Θ§Γœ3=Γœ4Θ§«σ÷ΛΘΚADΓΈBE
÷ΛΟςΘΚΓΏABΓΈCDΘ®“―÷ΣΘ©
ΓύΓœ4=Γœ______Θ®______Θ©
ΓΏΓœ3=Γœ4Θ®“―÷ΣΘ©ΓύΓœ3=Γœ______Θ®______Θ©
ΓύΓœ1=Γœ2Θ®“―÷ΣΘ©ΓύΓœ1+ΓœCAF=Γœ2+ΓœCAFΘ®Β» ΫΒΡ–‘÷ Θ©
Φ¥ΓœBAF=ΓœDAC
ΓύΓœ3=Γœ______Θ®Β»ΝΩ¥ζΜΜΘ©
ΓύADΓΈBEΘ®______Θ©

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΫΪ“ΜΖυ»ΐΫ«ΑεΤ¥≥…»γΆΦΥυ ΨΒΡΆΦ–ΈΘ§ΙΐΒψCΉςCFΤΫΖ÷ΓœDCEΫΜDE”ΎΒψFΘ°

Θ®1Θ©«σ÷ΛΘΚCFΓΈABΘ°
Θ®2Θ©«σΓœDFCΒΡΕ» ΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
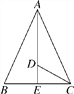
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΓςABC÷–Θ§“―÷ΣABΘΫACΘ§ΓœBACΚΆΓœACBΒΡΤΫΖ÷œΏœύΫΜ”ΎΒψDΘ§ΓœADCΘΫ125ΓψΘ§«σΓœACBΚΆΓœBACΒΡΕ» ΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ADΈΣΓςABCΒΡ÷–œΏΘ§BEΈΣΓςABDΒΡ÷–œΏΘ°
(1)»τΓœABEΘΫ15ΓψΘ§ΓœBADΘΫ40ΓψΘ§‘ρΓœBEDΘΫ________ΓψΘΜ
(2)«κ‘ΎΆΦ÷–Ής≥ωΓςBED÷–BD±Ώ…œΒΡΗΏEFΘΜ
(3)»τΓςABCΒΡΟφΜΐΈΣ40Θ§BDΘΫ5Θ§‘ρΒψEΒΫBC±ΏΒΡΨύάκΈΣΕύ…ΌΘΩ

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§÷±œΏABΓΔCDœύΫΜ”ΎΒψOΘ°“―÷ΣΓœBODΘΫ75ΓψΘ§OEΑ―ΓœAOCΖ÷≥…ΝΫΗωΫ«Θ§«“ΓœAOEΘΚΓœEOCΘΫ2ΘΚ3Θ°
Θ®1Θ©«σΓœAOEΒΡΕ» ΐΘΜ
Θ®2Θ©»τOFΤΫΖ÷ΓœBOEΘ§Έ ΘΚOB «ΓœDOFΒΡΤΫΖ÷œΏ¬πΘΩ ‘ΥΒΟςάμ”…Θ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΘ§÷±œΏABΓΈDCΘ§ΒψPΈΣΤΫΟφ…œ“ΜΒψΘ§Ν§Ϋ”AP”κCPΘ°



Θ®1Θ©»γΆΦ1Θ§ΒψP‘Ύ÷±œΏABΓΔCD÷°ΦδΘ§Β±ΓœBAP=60ΓψΘ§ΓœDCP=20Γψ ±Θ§«σΓœAPCΘ°
Θ®2Θ©»γΆΦ2Θ§ΒψP‘Ύ÷±œΏABΓΔCD÷°ΦδΘ§ΓœBAP”κΓœDCPΒΡΫ«ΤΫΖ÷œΏœύΫΜ”ΎΒψKΘ§–¥≥ωΓœAKC”κΓœAPC÷°ΦδΒΡ ΐΝΩΙΊœΒΘ§≤ΔΥΒΟςάμ”…Θ°
Θ®3Θ©»γΆΦ3Θ§ΒψP¬δ‘ΎCDΆβΘ§ΓœBAP”κΓœDCPΒΡΫ«ΤΫΖ÷œΏœύΫΜ”ΎΒψKΘ§ΓœAKC”κΓœAPC”–ΚΈ ΐΝΩΙΊœΒΘΩ≤ΔΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com