
【题目】如图1,正方形ABCD的边长为4,点E, F分别在BC, BD上,且BE=1,过三点C, E, F作⊙O交CD于点G.

(1)证明∠EFG =90°.
(2)如图2,连结AF,当点F运动至点A,F, G三点共线时,求![]() 的面积.
的面积.
(3)在点F整个运动过程中,
①当EF, FG, CG中满足某两条线段相等,求所有满足条件的BF的长.
②连接EG,若![]() 时,求⊙O的半径(请直接写出答案) .
时,求⊙O的半径(请直接写出答案) .
【答案】(1)证明见解析;(2)3;(3)①![]() , 2
, 2![]() ,
,![]() ;②
;②![]() .
.
【解析】
(1)连结EG,根据∠C=90°可得EG为⊙O的直径,进而可得结论;
(2)过点F作AD的垂线分别交AD,BC于点M,N,设MF=MD=a,求出EN=3-a,然后证明△AMF≌△FNE,得到MF=EN,求出a的值即可;
(3)①分情况讨论:当EF=CG 时;当EF=FG时;当FG=CG时,分别作出图形求出BF即可;②连接EG,过点E作EH⊥BD于点H,过点G作GI⊥BD于I,根据正方形的性质求出BD、BH、HE的长,然后证明△HEF∽△IFG,利用相似三角形的性质求出IF,进而得到HF的长,再利用勾股定理求出EF和EG即可解决问题.
解:(1)连结EG,
∵∠C=90°,
∴EG为⊙O的直径,
∴∠EFG=90°;
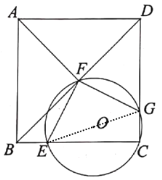
(2)过点F作AD的垂线分别交AD,BC于点M,N,

由(1)得:∠AFE=∠EFG =90°,∠ADF=45°,
∴设 MF=MD=a,则MD=NC=a,
∴EN=4-1-a=3-a,
∵AD=MN,
∴AM=FN,
∵∠NFE+∠AFM=∠AFM+∠MAF,
∴∠NFE=∠MAF,
又∵∠AMF=∠FNE,
∴△AMF≌△FNE,
∴MF=EN,即a=3-a,
∴a=1.5,
∴![]() ;
;
(3)①当EF=CG 时,

易得EF∥CG,
∴∠BEF =∠C=90°,
∴BE=EF=1,
∴BF=![]() ;
;
当EF=FG时,

∵∠EFG=90°,
∴∠ECF=∠EGF=45°,且∠ACE=45°,
∴点A,C,F共线,
∴F为对角线的交点,
∴BF=![]() BD= 2
BD= 2![]() ;
;
当FG=CG时,

则EF=CE,即EF=CE=4-1=3,设FN=x,
由(2)可知AM=BN=x,
∴EN=x-1,
在Rt△ENF中,![]() ,即
,即![]() ,
,
解得:![]() ,
,![]() (不符合题意,舍去),
(不符合题意,舍去),
∴![]() ,
,
∴综上所述,所有满足条件的BF长为![]() ,2
,2![]() ,
,![]() ;
;
②如图,连接EG,过点E作EH⊥BD于点H,过点G作GI⊥BD于I,
∵正方形ABCD的边长为4,BE=1,
∴BD=![]() ,BH=HE=
,BH=HE=![]() ,
,
∵∠EFG=∠EHF=∠GIF=90°,
∴∠HFE+∠GFI=90°,∠HFE+∠HEF=90°,
∴∠GFI=∠HEF,
∴△HEF∽△IFG,
∴![]() ,
,
∴![]() ,ID=IG=2HF,
,ID=IG=2HF,
∴BD=BH+HF+IF+ID=![]() ,
,
∴![]() ,
,
∴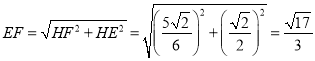 ,
,
∴![]() ,
,
∴ ,
,
∵EG为直径,
∴⊙O的半径为![]() .
.



 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:
【题目】定义:有且仅有一组对角相等的凸四边形叫做“准平行四边形”.例如:凸四边形![]() 中,若
中,若![]() ,则称四边形
,则称四边形![]() 为准平行四边形.
为准平行四边形.
(1)如图①,![]() 是
是![]() 上的四个点,
上的四个点,![]() ,延长
,延长![]() 到
到![]() ,使
,使![]() .求证:四边形
.求证:四边形![]() 是准平行四边形;
是准平行四边形;

(2)如图②,准平行四边形![]() 内接于
内接于![]() ,
,![]() ,若
,若![]() 的半径为
的半径为![]() ,求
,求![]() 的长;
的长;

(3)如图③,在![]() 中,
中,![]() ,若四边形
,若四边形![]() 是准平行四边形,且
是准平行四边形,且![]() ,请直接写出
,请直接写出![]() 长的最大值.
长的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数y=ax2+bx+![]() (a>0,b<0)的图象与x轴只有一个公共点A.
(a>0,b<0)的图象与x轴只有一个公共点A.
(1)当a=![]() 时,求点A的坐标;
时,求点A的坐标;
(2)求A点的坐标(只含b的代数式来表示);
(3)过点A的直线y=x+k与二次函数的图象相交于另一点B,当b≥﹣1时,求点B的横坐标m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,勾股定理反映了直角三角形三条边的关系: a2+b2=c2, 而a2, b2, c2又可以看成是以a,b, c为边长的正方形的面积.如图,在Rt△ABC中,∠ACB=90°,BC=a, AC=b,O为AB的中点.分别以AC,BC 为边向△ABC外作正方形ACFG,BCED,连结OF, EF, OE,则△OEF的面积为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)经过点A(-3,2),B(0,-2)其对称轴为直线x=![]() ,C(0,
,C(0, ![]() )为y轴上一点,直线AC与抛物线交于另一点D,
)为y轴上一点,直线AC与抛物线交于另一点D,
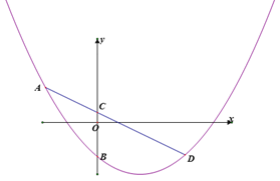
(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在点F使△ADF是直角三角形,如果存在,求出点F的坐标,如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OC是△ABC中AB边的中线,∠ABC=36°,点D为OC上一点,如果OD=kOC,过D作DE∥CA交于BA点E,点M是DE的中点,将△ODE绕点O顺时针旋转α度(其中0°<α<180°)后,射线OM交直线BC于点N.
(1)如果△ABC的面积为26,求△ODE的面积(用k的代数式表示);
(2)当N和B不重合时,请探究∠ONB的度数y与旋转角α的度数之间的函数关系式;
(3)写出当△ONB为等腰三角形时,旋转角α的度数.
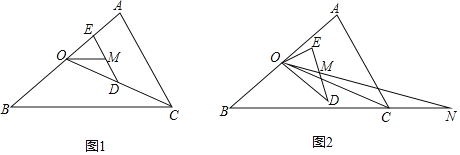
查看答案和解析>>
科目:初中数学 来源: 题型:
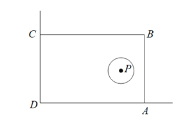
【题目】在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用26m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设BC=x m.
(1)若矩形花园ABCD的面积为165m2,求 x的值;
(2)若在P处有一棵树,树中心P与墙CD,AD的距离分别是13m和6m,要将这棵树围在花园内(考虑到树以后的生长,篱笆围矩形ABCD时,需将以P为圆心,1为半径的圆形区域围在内),求矩形花园ABCD面积S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() (
(![]() 在
在![]() 的左侧)与
的左侧)与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() 、
、![]() .
.

(1)如图1,点![]() 是直线
是直线![]() 上方抛物线上一点,当
上方抛物线上一点,当![]() 面积最大时,点
面积最大时,点![]() 分别为
分别为![]() 轴上的动点,连接
轴上的动点,连接![]() 、
、![]() 、
、![]() ,求
,求![]() 的周长最小值;
的周长最小值;
(2)如图2,点![]() 关于
关于![]() 轴的对称点为点
轴的对称点为点![]() ,将抛物线沿射线
,将抛物线沿射线![]() 的方向平移得到新的拋物线
的方向平移得到新的拋物线![]() ,使得
,使得![]() 交
交![]() 轴于点
轴于点![]() (
(![]() 在
在![]() 的左侧). 将
的左侧). 将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 至
至![]() . 抛物线
. 抛物线![]() 的对称轴上有—动点
的对称轴上有—动点![]() ,坐标系内是否存在一点
,坐标系内是否存在一点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形,若存在,请直接写出点
为顶点的四边形是菱形,若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com