
(本题8分)如图,已知在⊙O中,∠ABD=∠CDB。
(1)求证:AB=CD;
(2)顺次连结ACBD四点,猜想得到的是哪种特殊的四边形?并说明理由。
(1)连结BC、AD,
∵∠ABD=∠CDB,∠A=∠C,BD=BD,
∴△ABD≌△BCD,∴AB=CD。
(2)得到的四边形是等腰梯形。
∵∠ACD=∠ABD,而∠ABD=∠CDB,
∴∠ACD=∠CDB,∴AC∥BD,
又∵∠ABD=∠CDB,∴AD=CB,
∴四边形ACBD是等腰梯形。
解析试题分析:(1)由优弧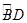 所对应的圆周角相等,推出∠A=∠C,又由题目所给出的∠ABD=∠CDB以及公共边,推出两个三角形全等,进而推出AB=CD。
所对应的圆周角相等,推出∠A=∠C,又由题目所给出的∠ABD=∠CDB以及公共边,推出两个三角形全等,进而推出AB=CD。
(2)又∠ACD=∠ABD与∠ABD=∠CDB等量代换,推出∠ACD=∠CDB,根据内错角相等,推出AC∥BD,又因为∠ABD=∠CDB,所以两个角所对应的劣弧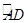 =
=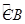 ,所以AD=CB,从而推出四边形为等腰梯形。
,所以AD=CB,从而推出四边形为等腰梯形。
考点:圆内周角
点评:通过圆周角相等推出弧相等,进而求出相关的数据。


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:
(本题8分)
如图,已知抛物线![]() 与直线y=x交于A、B两点,与y轴交于点C,OA=OB,BC∥x轴
与直线y=x交于A、B两点,与y轴交于点C,OA=OB,BC∥x轴
(1)求抛物线的解析式.
(2)设D、E是线段AB上异于A、B的两个动点(点E在点D的上方),DE=![]() ,过D、E两点分别作y轴的平行线,交抛物线于F、G,若设D点的横坐标为x,四边形DEGF的面积为y,求x与y之间的关系式,写出自变量x的取值范围,并回答x为何值时,y有最大值.
,过D、E两点分别作y轴的平行线,交抛物线于F、G,若设D点的横坐标为x,四边形DEGF的面积为y,求x与y之间的关系式,写出自变量x的取值范围,并回答x为何值时,y有最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
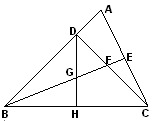
 中,
中,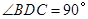 ,
,  平分
平分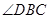 ,与
,与 相交于点
相交于点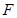 ,延长
,延长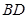 到
到 ,使
,使 ,
,
 ;
; 交
交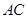 于
于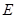 ,且
,且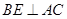 ,)试说明:
,)试说明: ;
;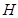 是
是 边的中点,连结
边的中点,连结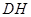 与
与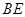 相交于点
相交于点 .
. ,
,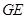 ,
,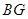 之间的数量关系,并说明理由
之间的数量关系,并说明理由查看答案和解析>>
科目:初中数学 来源:2012届湖北省黄石四中七年级下学期期中考试数学卷 题型:解答题
(本题6分)如图,已知∠1 =∠2,∠B =∠C,可推得AB∥CD。
理由如下:
∵∠1 =∠2(已 知),
且∠1 =∠CGD(__________________________)
∴∠2 =∠CGD(等量代换)
∴CE∥BF(_______________________________)
∴∠ =∠BFD(__________________________)
又∵∠B =∠C(已 知)
∴∠BFD =∠B( )
∴AB∥CD(________________________________)
查看答案和解析>>
科目:初中数学 来源:2012-2013学年浙江省杭州市九年级12月月考数学试卷(解析版) 题型:解答题
(本题8分)如图,已知点P是反比例函数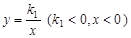 图像上一点,过点P作x轴、y轴的垂线,分别交x轴、y轴于A、B两点,交反比例函数
图像上一点,过点P作x轴、y轴的垂线,分别交x轴、y轴于A、B两点,交反比例函数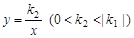 图像于E、F两点.
图像于E、F两点.
(1) 用含k1、k2的式子表示以下图形面积:
① 四边形PAOB;② 三角形OFB;③ 四边形PEOF;
(2) 若P点坐标为(-4,3),且PB︰BF=2︰1,分别求出 、
、 的值.
的值.

查看答案和解析>>
科目:初中数学 来源:2011-2012学年浙江省九年级上学期期中阶段性测试数学卷 题型:解答题
(本题14分)如图,已知正比例函数和反比例函数的图象都经过点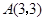 .
.

(1)求正比例函数和反比例函数的解析式;
(2)把直线OA向下平移后与反比例函数的图象交于点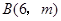 ,求
,求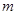 的值和这个一次函数的解析式;
的值和这个一次函数的解析式;
(3)第(2)问中的一次函数的图象与 轴、
轴、 轴分别交于C、D,求过A、B、D三点的二次函数的解析式;
轴分别交于C、D,求过A、B、D三点的二次函数的解析式;
(4)在第(3)问的条件下,二次函数的图象上是否存在点E,使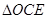 的面积
的面积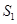 与
与 的面积S满足:
的面积S满足: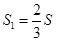 ?若存在,求点E的坐标;若不存在,请说明理由.
?若存在,求点E的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com