
【题目】如图,点0是等边△ABC内一点,∠AOB=110°,∠BOC=α,OC=CD,
且∠DOC=60°连接OD.
(1)求证:△COD是等边三角形
(2)当α=150°时,试判断△AOD的形状,并说明理由
(3)探究:当α为多少度时,△AOD是等腰三角形

【答案】(1)证明略。
(2)△AOD是直角三角形
(3)α=140°
【解析】(1)根据旋转的性质可得出OC=OD,结合题意即可证得结论;
(2)结合(1)的结论可作出判断;
(3)找到变化中的不变量,然后利用旋转及全等的性质即可做出解答.
(1)证明:∵将△BOC绕点C按顺时针方向旋转60°得△ADC
∴CO=CD,∠OCD=60°
∴△COD是等边三角形.
(2)解:当![]() =150°时,△AOD是直角三角形
=150°时,△AOD是直角三角形
理由是:∵△BOC≌△ADC
∴∠ADC=∠BOC=150°
又∵△COD是等边三角形
∴∠ODC=60°[来
∴∠ADO=∠ADC -∠ODC=90°,即△AOD是直角三角形.
(3)解:①要使AO=AD,需∠AOD=∠ADO
∵∠AOD= ![]() =
= ![]() ,∠ADO=
,∠ADO= ![]()
∴![]() =
= ![]()
∴![]()
②要使OA=OD,需∠OAD=∠ADO
∵∠OAD=![]() (∠AOD+∠ADO)=
(∠AOD+∠ADO)=![]() =
=![]()
∴![]() =
=![]()
∴![]()
③要使DO=DA,需∠OAD=∠AOD.
∵∠AOD= ![]() =
= ![]() ,∠OAD=
,∠OAD=![]() ∴
∴![]() =
=![]() ,解得
,解得![]()
综上所述:当![]() 的度数为
的度数为![]() 或
或![]() 或
或![]() 时,△AOD是等腰三角形.
时,△AOD是等腰三角形.
“点睛”本题以“空间与图形”中的核心知识(如等边三角形)的性质、全等三角形的性质与证明、直角三角形的判定、多边形内角和等)为载体,内容由浅入深,层层递进,试题中几何演绎推理的难度适中,蕴含着丰富的思想方法(如运动变化、数形结合、分类讨论、方程思想等)能较好地考查学生的推理、探究及解决问题的能力.


科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系中有A(-2,1),B(3,1),C(2,3)三点.请回答下列问题:
(1)在坐标系内描出点A,B,C的位置.
(2)求出以A,B,C三点为顶点的三角形的面积.
(3)在y轴上是否存在点P,使以A,B,P三点为顶点的三角形的面积为10?若存在,请直接写出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点O,与BC相交于点N,连接BM、DN.
(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求菱形BMDN的面积和对角线MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量某交通路口设立的路况显示牌的立杆AB的高度,在D处用高1.2m的测角仪CD,测得最高点A的仰角为32°,已知观测点D到立杆AB的距离DB为3.8m,求立杆AB的高度.(结果精确到0.1m)
【参考数据:sin32°=0.53,cos32°=0.85,tan32°=0.62】
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,AC=BC,D为边AB中点,点E、F分别在射线CA、BC上,且AE=CF,连结EF.
猜想:如图①,当点E、F分别在边CA和BC上时,线段DE与DF的大小关系为________.
探究:如图②,当点E、F分别在边CA、BC的延长线上时,判断线段DE与DF的大小关系,并加以证明.
应用:如图②,若DE=4,利用探究得到的结论,求△DEF的面积.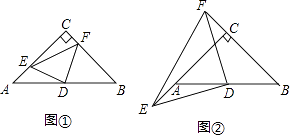
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC由△A′B′C′绕O点旋转180°而得到,则下列结论不成立的是( )
A.点A与点A′是对应点
B.BO=B′O
C.∠ACB=∠C′A′B′
D.AB∥A′B′
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知D、E分别为△ABC中AB、BC上的动点,直线DE与直线AC相交于F,∠ADE的平分线与∠B的平分线相交于P,∠ACB的平分线与∠F的平分线相交于Q.
(1)如图1,当F在AC的延长线上时,求∠P与∠Q之间的数量关系;
(2)如图2,当F在AC的反向延长线上时,求∠P与∠Q之间的数量关系(用等式表示).
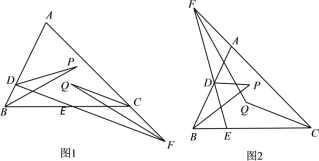
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线,DE⊥AB于点E.
(1)如图1,连接EC,求证:△EBC是等边三角形;
(2)点M是线段CD上的一点(不与点C,D重合),以BM为一边,在BM的下方作∠BMG=60°,MG交DE延长线于点G.求证:AD=DG+MD;
(3)点N是线段AD上的一点,以BN为一边,在BN的下方作∠BNG=60°,NG交DE延长线于点G.请在图3中画出图形,并直接写出ND,DG与AD数量之间的关系.
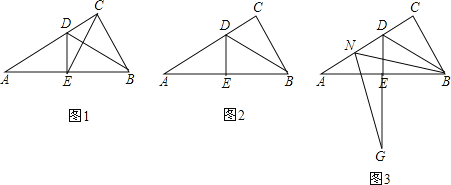
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com