
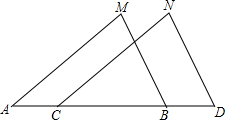
 如图,已知MB=ND,MB∥ND,添加下列条件后,仍不能判定△ABM≌△CDN的是( )
如图,已知MB=ND,MB∥ND,添加下列条件后,仍不能判定△ABM≌△CDN的是( )| A. | AM=CN | B. | AC=BD | C. | ∠M=∠N | D. | AM∥CN |
分析 先由MB∥ND,可得∠MBA=∠NDC,再根据全等三角形的判定方法:SSS、SAS、ASA、AAS、HL,结合选项进行判定,然后选择不能判定全等的选项.
解答 解:∵MB∥ND,
∴∠MBA=∠NDC.
A、添加条件AM=CN,仅满足SSA,不能判定两个三角形全等;
B、由AC=BD,可得AB=CD,符合SAS,能够判定△ABM≌△CDN;
C、添加条件∠M=∠N,可用ASA判定△ABM≌△CDN;
D、由AM∥CN,可得∠A=∠NCD,可用AAS判定△ABM≌△CDN.
故选A.
点评 本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
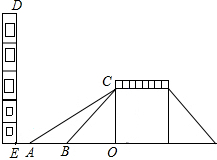 如图是某一过街天桥的示意图,天桥高CO为6米,坡道倾斜角∠CBO为45°,在距B点5米处有一建筑物DE.为方便行人上下天桥,市政部门决定减少坡道的倾斜角,但要求建筑物与新坡角A处之间地面要留出不少于3米宽的人行道.
如图是某一过街天桥的示意图,天桥高CO为6米,坡道倾斜角∠CBO为45°,在距B点5米处有一建筑物DE.为方便行人上下天桥,市政部门决定减少坡道的倾斜角,但要求建筑物与新坡角A处之间地面要留出不少于3米宽的人行道.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
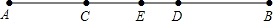 如图,已知AB=10cm,点C在线段AB上,且AC比BC短4cm.
如图,已知AB=10cm,点C在线段AB上,且AC比BC短4cm.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,∠C=90,∠CAB=60°,按以下步骤作图:①分别以A、B为圆心,以大于$\frac{1}{2}AB$的长为半径作弧,两弧相交于点P和Q;②作直线PQ交AB于点D,交BC于点E.若BE=6,则线段CE的长为3.
如图,在△ABC中,∠C=90,∠CAB=60°,按以下步骤作图:①分别以A、B为圆心,以大于$\frac{1}{2}AB$的长为半径作弧,两弧相交于点P和Q;②作直线PQ交AB于点D,交BC于点E.若BE=6,则线段CE的长为3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
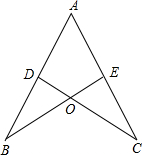 如图,已知AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.
如图,已知AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
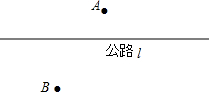 如图所示,A,B两村在公路l的两旁,现需在公路上修建一个汽车站,使车站到两村的距离相等,你能在公路l上确定这个车站的位置吗?(尺规作图作出P点的位置,不写作法,保留作图痕迹,写出结论)
如图所示,A,B两村在公路l的两旁,现需在公路上修建一个汽车站,使车站到两村的距离相等,你能在公路l上确定这个车站的位置吗?(尺规作图作出P点的位置,不写作法,保留作图痕迹,写出结论)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com