
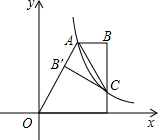
 如图,双曲线y=
如图,双曲线y=| 2 |
| x |
| 2 |
| x |
| 2 |
| a |
| 4 |
| a |
| 2 |
| x |
| 2 |
| x |
| 4 |
| a |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| 1 |
| 2 |
| a |
| 2 |
| 4 |
| a |
| 1 |
| 2 |
| 2 |
| a |


科目:初中数学 来源: 题型:
| 5 |
| x+1 |
| 4 |
| x-3 |
|
| 1 |
| x2-2x |
| 1 |
| x2-4x+4 |
| 2 |
| x2-2x |
查看答案和解析>>
科目:初中数学 来源: 题型:
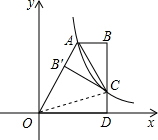
 在平面直角坐标系中,点B的坐标为(2,0),过点B作AB⊥x轴,交y=
在平面直角坐标系中,点B的坐标为(2,0),过点B作AB⊥x轴,交y=| m |
| x |
| m |
| 2 |
| m |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
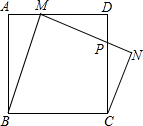 如图,正方形ABCD中,M为边AD的一动点(不与点A、D重合),作等腰梯形BMNC,其中BM∥CN,BC=MN,MN与CD交于点P,若AB=1,AM=x,CP=y,则y关于x的函数关系式为y=
如图,正方形ABCD中,M为边AD的一动点(不与点A、D重合),作等腰梯形BMNC,其中BM∥CN,BC=MN,MN与CD交于点P,若AB=1,AM=x,CP=y,则y关于x的函数关系式为y=查看答案和解析>>
科目:初中数学 来源: 题型:
| 测试项目 | 测试成绩 | ||
| 甲 | 乙 | 丙 | |
| 课堂教学 | 74 | 87 | 69 |
| 普通话 | 58 | 74 | 70 |
| 粉笔字 | 87 | 43 | 65 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com