
【题目】如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A′B′C′,M是BC的中点,P是A'B’的中点,连接PM,若BC=4,AC=3,则在旋转的过程中,线段PM的长度不可能是( )
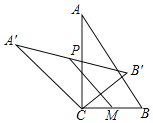
A.5B.4.5C.2.5D.0.5
 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
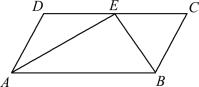
【题目】已知:如图,在四边形ABCD中,AD∥BC,点E为CD边上一点,AE与BE分别为∠DAB和∠CBA的平分线.
(1)作线段AB的垂直平分线交AB于点O,并以AB为直径作⊙O(要求:尺规作图,保留作图痕迹,不写作法);
(2)在(1)的条件下,⊙O交边AD于点F,连接BF,交AE于点G,若AE=4,sin∠AGF=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两辆汽车同时从相距330千米的甲、乙两地相向而行,s(千米)表示汽车与甲地的距离,t(分)表示汽车行驶的时间,如图,L1,L2分别表示两辆汽车的s与t的关系.
(1)L1表示哪辆汽车到甲地的距离与行驶时间的关系?
(2)汽车B的速度是多少?
(3)求L1,L2分别表示的两辆汽车的s与t的关系式.
(4)2小时后,两车相距多少千米?
(5)行驶多长时间后,A、B两车相遇?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E、F、G、H分别是四边形ABCD边AB、BC、CD、AD的中点,下列说法正确的是( )
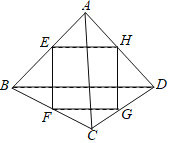
A.当AC⊥BD时,四边形EFGH是菱形
B.当AC=BD时,四边形EFGH是矩形
C.当四边形ABCD是平行四边形时,则四边形EFGH是矩形
D.当四边形ABCD是矩形时,则四边形EFGH是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,吊车在水平地面上吊起货物时,吊绳BC与地面保持垂直,吊臂AB与水平线的夹角为64°,吊臂底部A距地面1.5m.(计算结果精确到0.1m,参考数据sin64°≈0.90,cos64°≈0.44,tan64°≈2.05)
(1)当吊臂底部A与货物的水平距离AC为5m时,吊臂AB的长为 m.
(2)如果该吊车吊臂的最大长度AD为20m,那么从地面上吊起货物的最大高度是多少?(吊钩的长度与货物的高度忽略不计)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 与x轴交于点A、B(点A在点B的左边), 点P在抛物线上.
与x轴交于点A、B(点A在点B的左边), 点P在抛物线上.
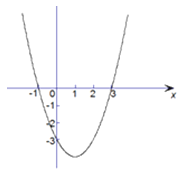
(1)点C是x轴上一个动点,四边形ACPQ是正方形,则满足条件 的点Q的坐标是______.
(2)连结AP,以AP为一条对角线作平行四边形AMPN,使点M在 以点(1,0),(0,1)为端点的线段上,则当点N的纵坐标取最小值时,N的坐标为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,平行四边形ABCD,对角线AC与BD相交于点E,点G为AD的中点,且AG=AB、CG的延长线交BA的延长线于点F,连接FD.试探究当∠BCD= °时,四边形ACDF是矩形,证明你的结论.
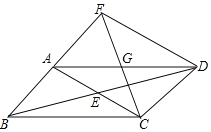
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接CC′.若∠CC′B′=32°,则∠B的大小是( )
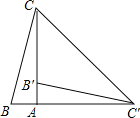
A.32°B.64°C.77°D.87°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在![]() 中,
中,![]() ,
,![]() 于
于![]() ,
,![]() 的平分线交
的平分线交![]() 于
于![]() ,交
,交![]() 于
于![]() ,
,![]() 的角平分线
的角平分线![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() .
.
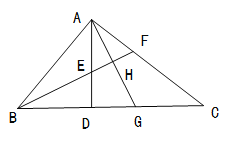
(1)求证:![]() ;
;
(2)判断![]() 与
与![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
(3)再找出二组相等的线段:①________;②___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com