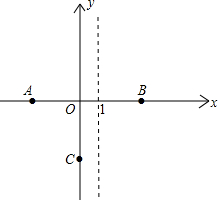
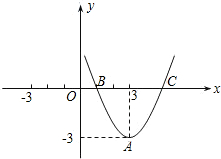
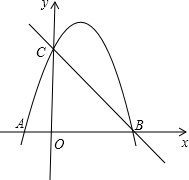
£Ø1£©ÉčÅ×ĪļĻß½āĪöŹ½ĪŖy=ax
2+bx£Øa”Ł0£©£¬½«A£®Bµć×ų±ź“śČėµĆ³ö£ŗ
£¬
½āµĆ£ŗ
£¬
¹Ź¾¹żO”¢A”¢BČżµćµÄÅ×ĪļĻß½āĪöŹ½ĪŖ£ŗy=-
x
2+
x£®
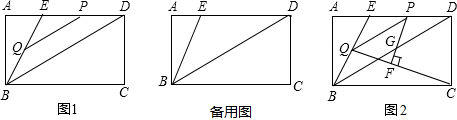
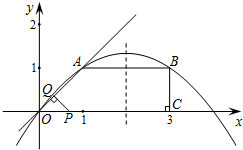
£Ø2£©¢Łµ±0£¼t”Ü2Ź±£¬ÖŲµž²æ·ÖĪŖ”÷OPQ£¬¹żµćA×÷AD”ĶxÖįÓŚµćD£¬
ČēĶ¼1£®
ŌŚRt”÷AODÖŠ£¬AD=OD=1£¬”ĻAOD=45”ć£®
ŌŚRt”÷OPQÖŠ£¬OP=t£¬”ĻOPQ=”ĻQOP=45”ć£®
”ąOQ=PQ=
t£®
”ąS=S
”÷OPQ=
OQ•PQ=
”Į
t”Į
t=
t
2£Ø0£¼t”Ü2£©£»
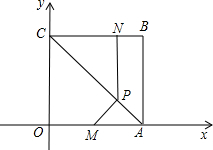
¢Śµ±2£¼t”Ü3Ź±£¬ÉčPQ½»ABÓŚµćE£¬ÖŲµž²æ·ÖĪŖĢŻŠĪAOPE£¬

×÷EF”ĶxÖįÓŚµćF£¬ČēĶ¼2£®”ß”ĻOPQ=”ĻQOP=45”ć
”ąĖıߊĪAOPEŹĒµČŃüĢŻŠĪ”ąAE=DF=t-2£®
”ąS=S
ĢŻŠĪAOPE=
£ØAE+OP£©•AD=
£Øt-2+t£©”Į1
=t-1£Ø2£¼t”Ü3£©£»
¢Ūµ±3£¼t£¼4Ź±£¬ÉčPQ½»ABÓŚµćE£¬½»BCÓŚµćF£¬
ÖŲµž²æ·ÖĪŖĪå±ßŠĪAOCFE£¬ČēĶ¼3£®
”ßB£Ø3£¬1£©£¬OP=t£¬”ąPC=CF=t-3£®
”ß”÷PFCŗĶ”÷BEF¶¼ŹĒµČŃüÖ±½ĒČż½ĒŠĪ

”ąBE=BF=1-£Øt-3£©=4-t
”ąS=S
Īå±ßŠĪAOCFE=S
ĢŻŠĪOABC-S
”÷BEF£¬
=
£Ø2+3£©”Į1-
£Ø4-t£©
2=-
t
2+4t-
£Ø3£¼t£¼4£©£»
£Ø3£©Į¬½ÓQC£¬OB£¬
ӧAB
”ĪOC£¬
”ą”ĻBAO+”ĻAOC=180”ć£¬
”ß”ĻAOC=45”ć£¬”ĻOQP=90”ć£¬
”ą”ĻQPO=45”ć£¬
”ß”ĻQPO+”ĻQPC=180”ć£¬
”ą”ĻBAO=”ĻQPC£¬
Ö»ŅŖ
=
»ņÕß
=
¼“æÉµĆ³öŅŌC”¢P”¢QĪŖ¶„µćµÄČż½ĒŠĪÓė”÷OABĻąĖĘ£¬
µĆ³ö£ŗ3-t=
”Į
t»ņ3-t=
”Į
t
½āµĆ£ŗt=2»ņt=
£»

£Ø4£©“ęŌŚ£¬t
1=1£¬t
2=2£®
½«”÷OPQČĘ×ŵćPĖ³Ź±ÕėŠż×Ŗ90”ć£¬“ĖŹ±Q£Øt+
£¬
£©£¬O£Øt£¬t£©
¢Łµ±µćQŌŚÅ×ĪļĻßÉĻŹ±£¬
=-
”Į£Øt+
£©
2+
”Į£Øt+
£©£¬
½āµĆt=2£»
¢Śµ±µćOŌŚÅ×ĪļĻßÉĻŹ±£¬t=-
t
2+
t£¬
½āµĆ£ŗt=1£®








 µ¼Ń§½Ģ³ĢøßÖŠŠĀæĪ±źĻµĮŠ“š°ø
µ¼Ń§½Ģ³ĢøßÖŠŠĀæĪ±źĻµĮŠ“š°ø
 Ć껿µČÓŚŅŌµćA”¢P0”¢B”¢CĪŖ¶„µćµÄĖıߊĪĆ껿µÄČż·ÖÖ®Ņ»£æČō“ęŌŚ£¬ĒėĒó³öĖłÓŠ·ūŗĻĢõ¼žµÄµćMµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
Ć껿µČÓŚŅŌµćA”¢P0”¢B”¢CĪŖ¶„µćµÄĖıߊĪĆ껿µÄČż·ÖÖ®Ņ»£æČō“ęŌŚ£¬ĒėĒó³öĖłÓŠ·ūŗĻĢõ¼žµÄµćMµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®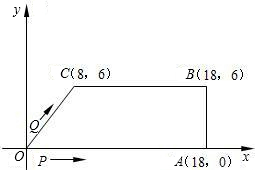

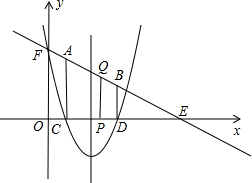 ĒóĖıߊĪPQFCµÄĆ껿SÓėtÖ®¼äµÄŗÆŹż¹ŲĻµŹ½£¬²¢Č·¶ØtµÄȔֵ·¶Ī§£®
ĒóĖıߊĪPQFCµÄĆ껿SÓėtÖ®¼äµÄŗÆŹż¹ŲĻµŹ½£¬²¢Č·¶ØtµÄȔֵ·¶Ī§£®