Question

4．在⊙O中，弦AB、CD相交于点E，连接AC、BC，AC=BC，AB=CD．
（1）如图1，求证：BE平分∠CBD；
（2）如图2，F为BC上一点，连接AF交CD于点G，当∠FAB=$\frac{1}{2}$∠ACB时，求证：AC=BD+2CF；
（3）如图3，在（2）的条件下，若S_△ACF=S_△CBD，⊙O的半径为3$\sqrt{6}$，求线段GD的长．

Answer 1

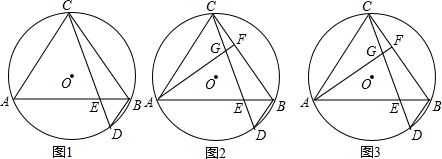
分析 （1）由AB=CD，得到$\widehat{AD}$=$\widehat{BC}$，由AC=BC，得到$\widehat{AC}$=$\widehat{BC}$，于是得到$\widehat{AD}$=$\widehat{AC}$，根据圆周角定理即可证得结论．
（2）根据全等三角形的性质得到∠CAB=∠CBA，根据三角形的内角和得到∠CBA+$\frac{1}{2}$∠ACB=90°推出AF⊥CH，得到∠ACB=∠AHC，根据圆内接四边形的性质得到∠ACB+∠ADB=180°，等量代换得到∠AHB=∠ADB，根据全等三角形的性质得到BD=BH，即可得到结论；
（3）根据已知条件得到AC∥BD，根据平行线的性质得到∠CBK=∠ACB，∠CKB=∠AFC，推出△AFC≌△CKB，于是得到S_△AFC=S_△CKB=S_△CBD，等量代换得到AC=3CF=3BD，设BD=CF=k，则AC=BC=3k，BF=2k，根据勾股定理得到AF=2$\sqrt{2}$k，由圆周角定理得到∠CAM=90°，解直角三角形得到AM=$\frac{3}{2}\sqrt{2}$k，根据勾股定理列方程得到AC=12，CF=4，AF=8$\sqrt{2}$，解直角三角形即可得到结论．

解答 （1）证明：∵AB=CD，
∴$\widehat{ADB}$=$\widehat{CBD}$，
∴$\widehat{AD}$=$\widehat{BC}$，
∵AC=BC，
∴$\widehat{AC}$=$\widehat{BC}$，
∴$\widehat{AD}$=$\widehat{AC}$，
∴∠ABC=∠ABD，
∴BE平分∠CBD；

（2）证明：如图2，在线段BF上取点H，使FH=FC，连接AH，AD，
∵AC=BC，∴∠CAB=∠CBA，
∵在△ABC中，∠CAB+∠CBA+∠ACB=180°，
∴∠CBA+$\frac{1}{2}$∠ACB=90°，
∵∠FAB=$\frac{1}{2}$∠ACB，
∴∠FAB+∠CBA=90°，
∴∠AFB=90°，
∴AF⊥CH，
∵CF=FH，
∴AC=AH，
∴∠ACB=∠AHC，
∵A、C、B、D四点在⊙O上，
∴∠ACB+∠ADB=180°，
∵∠AHC+∠AHB=180°，
∴∠AHB=∠ADB，
∵∠ABC=∠ABD，AB=AB，
在△AHB与△ADB中，
$\left\{\begin{array}{l}{∠AHB=∠ADB}\\{∠ABH=∠ABD}\\{AB=AB}\end{array}\right.$，
∴△AHB≌△ADB，
∴BD=BH，
∵AC=BC=CF+FH+HB，
∴AC=BD+2CF；

（3）解：如图3，过点C作CK⊥BD于点K，作直径CM，连接AM，
∵∠CBA=∠CAB=∠ABD，
∴AC∥BD，
∴∠CBK=∠ACB，∠CKB=∠AFC，AC=BC，
在△AFC与△CKB中，$\left\{\begin{array}{l}{∠CBK=∠ACB}\\{∠CKB=∠AFC}\\{AC=BC}\end{array}\right.$，
∴△AFC≌△CKB，
∴S_△AFC=S_△CKB=S_△CBD，
∴BD=BK=CF，
∵AC=BD+2CF，
∴AC=3CF=3BD，
设BD=CF=k，则AC=BC=3k，BF=2k，
在Rt△ACF中，由勾股定理得：AF=2$\sqrt{2}$k，
在Rt△AFB中，tan∠FBA=$\frac{AF}{BF}=\sqrt{2}$，
∵CM为⊙O的直径，
∴∠CAM=90°，
∵∠CMA=∠CBA，
在Rt△ACM中，AC=3k，tan∠CMA=$\sqrt{2}$，CM=6$\sqrt{6}$，
∴AM=$\frac{3}{2}\sqrt{2}$k，
由勾股定理得：（3k）²+（$\frac{3}{2}\sqrt{2}k$）²=（6$\sqrt{6}$）²，
∴k=4，
∴AC=12，CF=4，AF=8$\sqrt{2}$，
在Rt△ACF中，tan∠CAF=$\frac{CF}{AF}=\frac{\sqrt{2}}{4}$，tan∠ACD=$\sqrt{2}$，AC=12，
∴CG=$\frac{12\sqrt{3}}{5}$，
在Rt△AFB中，AF=8$\sqrt{2}$，FB=8，
由勾股定理得：AB=CD=8$\sqrt{3}$，
∴DG=$\frac{28\sqrt{3}}{5}$．

点评 本题考查了全等三角形的判定和性质，解直角三角形，圆周角定理，角平分线的定义，正确的作出辅助线构造全等三角形是解题的关键．