
分析 (1)先求抛物线的对称轴及点C坐标,证明△AOC∽△COB,得出OA•OB=4,由根与系数的关系:x1•x2
=$\frac{c}{a}$列式求出a的值,写出二次函数的解析式;
(2)过M作x轴的垂线,将△BCM分成了两个同底边的三角形,设点M的坐标为(a,-$\frac{1}{2}$a2+$\frac{3}{2}$a+2),则N(a,0),表示出DM的长,利用面积公式代入求出△BCM的面积=△DCM的面积+△BDM的面积,得出一个二次函数,求最值即可;
(3)分四种情况进行讨论:因为△ACB是直角三角形,且两直角边的比为1:2,所以使△BCP与△ABC相似时,△BCP必有一个角是直角,当∠BPC为直角时,可利用直角所对的圆周角是直角画辅助圆构建直角△BCP,即图3和图4;因此当三个顶点分别是直角时,列式进行计算,发现只有一种情况成立,从而得出结论.
解答 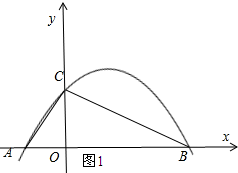 解:(1)对称轴x=$\frac{3a}{2a}$=$\frac{3}{2}$,
解:(1)对称轴x=$\frac{3a}{2a}$=$\frac{3}{2}$,
把x=0代入y=ax2-3ax+2,得y=2,
∴点C的坐标为(0,2),
∵当a>0时,抛物线与x轴交点均在x轴的正半轴,
∴△BAC为钝角三角形,
∴a>0不成立,
当a<0时,如图1所示,
∵∠ACO+∠OCB=90°,∠CAO+∠ACO=90°,
∴∠CAO=∠BCO,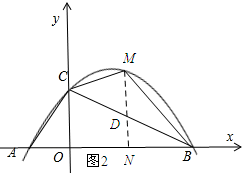
又∵∠AOC=∠BOC=90°,
∴△AOC∽△COB,
∴$\frac{AO}{OC}=\frac{OC}{OB}$,
∴OC2=OA•OB,
∵点C的坐标为(0,2),
∴OC=2,
∴OA•OB=4,
∴$\frac{2}{a}$=-4,
解得:a=-$\frac{1}{2}$,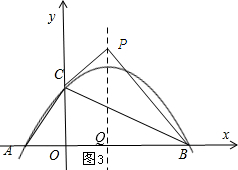
∴抛物线的解析式为y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2;
(2)存在,
如图2所示:过点M作MN⊥AB,垂足为N,MN交BC与点D,
∵令y=0得:-$\frac{1}{2}$x2+$\frac{3}{2}$x+2=0,解得:x=-1或x=4,
∴点B(4,0),
∴OB=4,
∴tan∠CBO=$\frac{1}{2}$,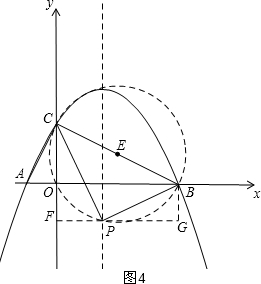
设点M的坐标为(a,-$\frac{1}{2}$a2+$\frac{3}{2}$a+2),则N(a,0),
∴BN=4-a,
∴DN=$\frac{1}{2}$NB=2-$\frac{1}{2}$a,
∴DM=-$\frac{1}{2}$a2+$\frac{3}{2}$a+2-2+$\frac{1}{2}$a=-$\frac{1}{2}$a2+2a,
∴△BCM的面积=$\frac{1}{2}$×4×(-$\frac{1}{2}$a2+2a)=-a2+4a=-(a-2)2+4,
∴当a=2时,△BCM的面积有最大,
∴M的坐标为(2,3);
(3)设点P的坐标为($\frac{3}{2}$,a).
分四种情况讨论:
①当△PCB∽△CAB时,如图3,∠ACB=∠BPC=90°,
∴∠ABC=∠CBP,
∵BC=BC,∠COB=∠CPB,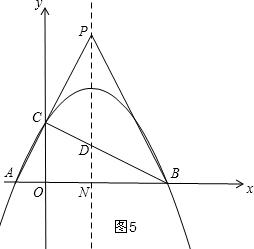
∴△COB≌△CPB,
∴PB=OB=4,
∵BQ=4-$\frac{3}{2}$=$\frac{5}{2}$,
由勾股定理得:PQ=$\sqrt{{4}^{2}-(\frac{5}{2})^{2}}$=$\frac{\sqrt{39}}{2}$,
∴P($\frac{3}{2}$,$\frac{\sqrt{39}}{2}$),
②当∠BPC=90°,点P在线段BC的下方时,如图4,
分别过P、B向y轴、x轴作垂线FG、BG,
则△CFP∽△PGB,
∵△BCP与与△ABC相似,
∴$\frac{FC}{PG}=\frac{FP}{BG}$=2或$\frac{1}{2}$,
即$\frac{2-a}{\frac{5}{2}}$=$\frac{\frac{3}{2}}{-a}$=2或$\frac{1}{2}$,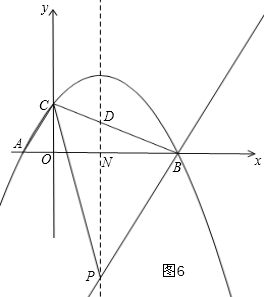
此方程无解;
③如图5,延长AC交对称轴于点P,则∠PCB=90°,
根据对称性可知:PN是AB的垂直平分线,
∴PA=PB,
∴∠CAB=∠ABP,
∴∠CAB≠∠CBP,
∵tan∠CAB=$\frac{CO}{AO}$=2,
∴∠CAB≠60°,
∴∠CAB≠∠CPB,
∴此种情况△BCP与与△ABC不相似;
④如图6,当∠CBP=90°时,
∵∠CBO=∠OBP=90°,∠OCB+∠CBO=90°,
∴∠OBP=∠OCB,
∵∠COB=∠PNB=90°,
∴△COB∽△BNP,
∴$\frac{CO}{BN}=\frac{BC}{PB}$,
∴$\frac{2}{\frac{5}{2}}$=$\frac{BC}{PB}$,
∴$\frac{BC}{PB}$=$\frac{4}{5}$,
∵$\frac{AC}{BC}$=$\frac{1}{2}$,
∴△BCP与△ABC不相似,
综上所述,当P($\frac{3}{2}$,$\frac{\sqrt{39}}{2}$)时,△BCP与与△ABC相似.
点评 本题是二次函数的综合题,考查出了二次函数的性质和利用待定系数法求二次函数的解析式;当二次项系数和一次项系数有一个相同的字母系数时,根据公式可以求出对称轴;另外,本题求三角形面积的最值问题,想办法转化为二次函数问题,利用顶点坐标来求;对于两个三角形相似,对应边不确定的情况下,要分情况进行讨论.


 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}-{y}^{2}}{xy}$ | B. | $\frac{{x}^{2}-{y}^{2}}{2xy}$ | C. | $\frac{{x}^{2}+{y}^{2}}{xy}$ | D. | $\frac{{x}^{2}+{y}^{2}}{2xy}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
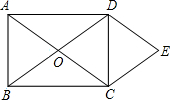 如图,O为矩形ABCD对角线的交点,AD=8cm,AB=6cm,将△ABO向右平移得到△DCE,则△ABO向右平移过程中扫过的面积是( )
如图,O为矩形ABCD对角线的交点,AD=8cm,AB=6cm,将△ABO向右平移得到△DCE,则△ABO向右平移过程中扫过的面积是( )| A. | 12cm2 | B. | 24cm2 | C. | 48cm2 | D. | 60cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com