
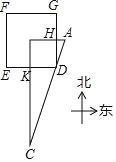
����Ŀ�����������������й���ͳ��ѧ����Ҫ����������������������������һ�����⣺�������ط����ٲ������п��ţ�������ʮ�岽��ľ���ʣ������ż������ľ�����ý���Ļ�˵�������ǣ���ͼ��DEFG��һ���߳�Ϊ200�����������ǹŴ��ij��ȵ�λ����������С�ǣ�����Hλ��GD���е㣬����Kλ��ED���е㣬������15����A����һ��ľ��������Ŷ��ٲ�ǡ�ÿ���λ��A������ľ������D��ֱ��AC�ϣ����������KC�ij�Ϊ���ٲ���

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������![]() �Ƿ���������
�Ƿ���������![]() ͼ����һ�㣬������˵����ȷ���ǣ� ��
ͼ����һ�㣬������˵����ȷ���ǣ� ��
A.ͼ��λ�ڶ���������
B.��![]() ʱ��
ʱ��![]() ��
��![]() ���������С
���������С
C.��![]() �ں���ͼ����
�ں���ͼ����
D.��![]() ʱ��
ʱ��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�������ͬѧ����һ�����������ϲ��ԣ����ֱ��涨����6������![]() ��6��
��6��![]() Ϊ�ϸ���9������
Ϊ�ϸ���9������![]() ��9��
��9��![]() Ϊ���㣬����ͬѧ�IJ��Գɼ����±���
Ϊ���㣬����ͬѧ�IJ��Գɼ����±���
�ɼ� | ��4 | ��5 | ��6 | ��7 | ��8 | ��9 |
������ | ��1 | ��2 | ��5 | ��2 | ��1 | ��4 |
������ | ��1 | ��1 | ��4 | ��5 | ��2 | ��2 |
�ֽ�����ͬѧ�IJ��Գɼ����Ƴ����²�������ͳ��ͼ����
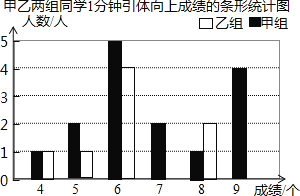
ͳ���� | ƽ���� | ��λ�� | ���� | ���� | �ϸ��� | ������ |
���� | a | 6 | 6 |
|
|
|
���� |
| b | 7 |
|
|
|
![]() ������ͳ��ͼ����������
������ͳ��ͼ����������
![]() ͳ�Ʊ��е�
ͳ�Ʊ��е�![]() ______��
______��![]() ______��
______��
![]() ��˵����������ʸ������������ʣ����Լ���ɼ�������ɼ��ã���Ҳ����˵����ɼ��ȼ���ɼ��ã������������֧������ɼ��õ����ɣ�
��˵����������ʸ������������ʣ����Լ���ɼ�������ɼ��ã���Ҳ����˵����ɼ��ȼ���ɼ��ã������������֧������ɼ��õ����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
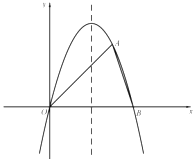
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�ֱ��AB��������y��ax2+bx���ڵ�A��6��0���͵�B��1����5����
��1�������������ߵı���ʽ��ֱ��AB�ı���ʽ��
��2�������C��ֱ��AB�ϣ��ҡ�BOC������ֵ��![]() �����C�����꣮
�����C�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ![]() �У�������
��������![]() ��
��![]() �ύ��ԭ��
�ύ��ԭ��![]() �͵�
�͵�![]() ����
����![]() ���������ϣ�
���������ϣ�
��1���������ߵı���ʽ����д�����ĶԳ��
��2����![]() ��ֵ��
��ֵ��
��3����![]() �������ߵĶԳ����ϣ����
�������ߵĶԳ����ϣ����![]() �����
�����![]() �����꣮
�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
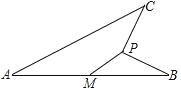
����Ŀ����ͼ���߶� AB��4��M Ϊ AB ���е㣬���� P ���� M �ľ����� 1������ PB���߶�
PB �Ƶ� P ��ʱ����ת 90���õ��߶� PC������ AC�����߶� AC ���ȵ����ֵ��_________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
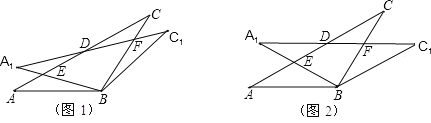
����Ŀ���ڡ�ABC �У�AB=BC=2����ABC=120�㣬����ABC �Ƶ� B ˳ʱ����ת������0�㣼����90�㣩�á�A1BC1��A1B �� AC �ڵ� E��A1C1 �ֱ� AC��BC �� D��F ���㣮
��1����ͼ 1���۲첢���룬����ת�����У��߶� EA1 �� FC ��������������ϵ�� ��֤����Ľ��ۣ�
��2����ͼ 2������=30��ʱ�����ж��ı��� BC1DA ����״����˵�����ɣ�
��3���ڣ�2��������£��� ED �ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
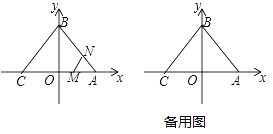
����Ŀ����ͼ����֪��ABC�Ķ�������ֱ�ΪA��3��0����B��0��4����C��-3��0��.����M��Nͬʱ��A�������M��A��C,N������A��B��C������ÿ��1����λ���ȵ��ٶ��ƶ�����һ�����㵽���յ�Cʱ����һ������Ҳ��ֹ֮ͣ�ƶ����ƶ�ʱ���Ϊt��.����MN.
��1����ֱ��BC�Ľ���ʽ��
��2���ƶ������У�����AMN��ֱ��MN���ۣ���Aǡ������BC���ϵ�D�������ʱtֵ����D�����ꣻ
��3������M,N�ƶ�ʱ������ABC��ֱ��MN�Ҳಿ�ֵ����ΪS����S����ʱ��t�ĺ�����ϵʽ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijС�ͼӹ�����ÿ�������ס����������͵IJ�Ʒ��1000����ԭ�ϳɱ������۵��ۣ������˼Ƽ����������
�ף�Ԫ/���� | �ң�Ԫ/���� | |
ԭ�ϳɱ� | 10 | 8 |
���۵��� | 20 | 16 |
�Ƽ����� | 2 | 1.5 |
��üӹ���ÿ���������Ͳ�Ʒx����ÿ����������ΪyԪ��
��1�����y��x֮��ĺ�����ϵʽ��
��2�����ù���ÿ��Ͷ���ܳɱ�������10750Ԫ���������żס����������͵�����������ʹ�ó�ÿ������õ�������������������ܳɱ���ԭ�ϳɱ�+�Ƽ����ʣ�������������һͶ���ܳɱ���
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com