Question

15．在学习了图形的旋转知识后，数学兴趣小组的同学们又进一步对图形旋转前后的线段之间、角之间的关系进行了探究．
（一）尝试探究
如图1，在四边形ABCD中，AB=AD，∠BAD=60°，∠ABC=∠ADC=90°，点E、F分别在线段BC、CD上，∠EAF=30°，连接EF．
（1）如图2，将△ABE绕点A逆时针旋转60°后得到△A′B′E′（A′B′与AD重合），请直接写出∠E′AF=30度，线段BE、EF、FD之间的数量关系为BE+DF=EF．
（2）如图3，当点E、F分别在线段BC、CD的延长线上时，其他条件不变，请探究线段BE、EF、FD之间的数量关系，并说明理由．
（二）拓展延伸
如图4，在等边△ABC中，E、F是边BC上的两点，∠EAF=30°，BE=1，将△ABE绕点A逆时针旋转60°得到△A′B′E′（A′B′与AC重合），连接EE′，AF与EE′交于点N，过点A作AM⊥BC于点M，连接MN，求线段MN的长度．

Answer 1

分析 （一）（1）根据图形旋转前后对应边相等，对应角相等，判定△AEF≌△AE′F，进而根据线段的和差关系得出结论；
（2）先在BE上截取BG=DF，连接AG，构造△ABG≌△ADF，进而利用全等三角形的对应边相等，对应角相等，判定△GAE≌△FAE，最后根据线段的和差关系得出结论；
（二）先根据旋转的性质判定△AEE′是等边三角形，进而利用等边△ABC、等边△AEE′的三线合一的性质，得到$\frac{AN}{AE}$=$\frac{AM}{AB}$和∠BAE=∠MAN，最后判定△BAE∽△MAN，并根据相似三角形对应边成比例，列出比例式求得MN的长．

解答 解：（一）（1）如图2，将△ABE绕点A逆时针旋转60°后得到△A′B′E′，则
∠1=∠2，BE=DE′，AE=AE′，
∵∠BAD=60°，∠EAF=30°，
∴∠1+∠3=30°，
∴∠2+∠3=30°，即∠FAE′=30°
∴∠EAF=∠FAE′，
在△AEF和△AE′F中，
$\left\{\begin{array}{l}{AE=AE′}\\{∠EAF=∠FAE′}\\{AF=AF}\end{array}\right.$，
∴△AEF≌△AE′F（SAS），
∴EF=E′F，即EF=DF+DE′，
∴EF=DF+BE，即线段BE、EF、FD之间的数量关系为BE+DF=EF，
故答案为：30，BE+DF=EF；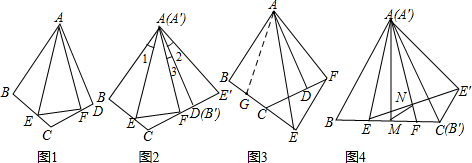


（2）如图3，在BE上截取BG=DF，连接AG，
在△ABG和△ADF中，
$\left\{\begin{array}{l}{AB=AD}\\{∠ABE=∠ADF}\\{BG=DF}\end{array}\right.$，
∴△ABG≌△ADF（SAS），
∴∠BAG=∠DAF，且AG=AF，
∵∠DAF+∠DAE=30°，
∴∠BAG+∠DAE=30°，
∵∠BAD=60°，
∴∠GAE=60°-30°=30°，
∴∠GAE=∠FAE，
在△GAE和△FAE中，
$\left\{\begin{array}{l}{AG=AF}\\{∠GAE=∠FAE}\\{AE=AE}\end{array}\right.$，
∴△GAE≌△FAE（SAS），
∴GE=FE，
又∵BE-BG=GE，BG=DF，
∴BE-DF=EF，
即线段BE、EF、FD之间的数量关系为BE-DF=EF；

（二）如图4，将△ABE绕点A逆时针旋转60°得到△A′B′E′，则
AE=AE′，∠EAE′=60°，
∴△AEE′是等边三角形，
又∵∠EAF=30°，
∴AN平分∠EAE'，
∴AN⊥EE′，
∴直角三角形ANE中，$\frac{AN}{AE}$=$\frac{\sqrt{3}}{2}$，
∵在等边△ABC中，AM⊥BC，
∴∠BAM=30°，
∴$\frac{AM}{AB}$=$\frac{\sqrt{3}}{2}$，且∠BAE+∠EAM=30°，
∴$\frac{AN}{AE}$=$\frac{AM}{AB}$，
又∵∠MAN+∠EAM=30°，
∴∠BAE=∠MAN，
∴△BAE∽△MAN，
∴$\frac{MN}{BE}$=$\frac{AM}{AB}$，即$\frac{MN}{1}$=$\frac{\sqrt{3}}{2}$，
∴MN=$\frac{\sqrt{3}}{2}$．

点评 本题以旋转为背景，考查了全等三角形与相似三角形，考核了学生对图形进行分解、组合的能力，解题关键是抓住图形旋转前后的对应边相等，对应角相等．解题时应注意等边三角形具有三线合一的性质，此类试题的一般解题方法为作辅助线构造全等三角形或相似三角形．