
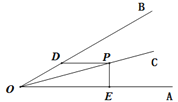
【题目】如图,∠AOB=30°,OC平分∠AOB,P为OC上任意一点,PD∥OA交OB于D,PE⊥OA于E,若OD=4,则PE= __________.
【答案】2
【解析】
过P作PF⊥OB于F,根据角平分线的定义可得∠AOC=∠BOC=15°,根据平行线的性质可得∠DPO=∠AOP=15°,从而可得PD=OD,再根据30度所对的边是斜边的一半可求得PF的长,最后根据角平分线的性质即可求得PE的长.
解:过P作PF⊥OB于F,
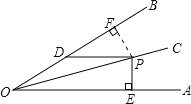
∵∠AOB=30°,OC平分∠AOB,
∴∠AOC=∠BOC=15°,
∵PD∥OA,
∴∠DPO=∠AOP=15°,
∴∠BOC=∠DPO,
∴PD=OD=4,
∵∠AOB=30°,PD∥OA,
∴∠BDP=30°,
∴在Rt△PDF中,PF=![]() PD=2,
PD=2,
∵OC为角平分线,PE⊥OA,PF⊥OB,
∴PE=PF,
∴PE=PF=2.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】根据给出的数轴及已知条件,解答下面的问题:
![]()
(1)已知点![]() ,
,![]() ,
,![]() 表示的数分别为1,
表示的数分别为1,![]() ,-3.观察数轴,与点
,-3.观察数轴,与点![]() 的距离为3的点表示的数是____,
的距离为3的点表示的数是____,![]() ,
,![]() 两点之间的距离为_____.
两点之间的距离为_____.
(2)数轴上,点![]() 关于点
关于点![]() 的对称点表示的数是_____.
的对称点表示的数是_____.
(3)若将数轴折叠,使得![]() 点与
点与![]() 点重合,则与
点重合,则与![]() 点重合的点表示的数是_____;若此数轴上
点重合的点表示的数是_____;若此数轴上![]() ,
,![]() 两点之间的距离为2019(
两点之间的距离为2019(![]() 在
在![]() 的左侧),且当
的左侧),且当![]() 点与
点与![]() 点重合时,
点重合时,![]() 点与
点与![]() 点也恰好重合,则点
点也恰好重合,则点![]() 表示的数是_____,点
表示的数是_____,点![]() 表示的数是_____;
表示的数是_____;
(4)若数轴上![]() ,
,![]() 两点间的距离为
两点间的距离为![]() (
(![]() 在
在![]() 左侧),表示数
左侧),表示数![]() 的点到
的点到![]() ,
,![]() 两点的距离相等,将数轴折叠,当
两点的距离相等,将数轴折叠,当![]() 点与
点与![]() 点重合时,点
点重合时,点![]() 表示的数是_____,点
表示的数是_____,点![]() 表示的数是_____(用含
表示的数是_____(用含![]() ,
,![]() 的式子表示这两个数).
的式子表示这两个数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个正整数可以表示为两个连续奇数的平方差,那么称该正整数为“和谐数”如(8=32﹣12,16=52﹣32,即8,16均为“和谐数”),在不超过2017的正整数中,所有的“和谐数”之和为( )
A. 255054 B. 255064 C. 250554 D. 255024
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知DE∥BC,BE平分∠ABC,∠C=65°,∠ABC=50°.
(1)求∠BED的度数;
(2)判断BE与AC的位置关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列两段材料,回答下列各题:
材料一:规定:求若干个相同的有理数(均不等于0)的除法运算叫做除方,如:![]() ,
,![]() 等,类比有理数的乘方,我们把
等,类比有理数的乘方,我们把![]() 记作
记作![]() ,读作“2的圈3次方”,
,读作“2的圈3次方”,![]() 记作
记作![]() ,读作“
,读作“![]() 的圈4次方”,一般地,把
的圈4次方”,一般地,把![]() 记作
记作![]() ,读作“
,读作“![]() 的圈
的圈![]() 次方”.
次方”.
材料二:求值:![]() . 解:设
. 解:设![]() ,将等式两边同时乘以2得:
,将等式两边同时乘以2得:![]() 将下式减去上式得
将下式减去上式得![]() 即
即![]()
(1)直接写出计算结果:![]()
(2)我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?试一试:将下列运算结果直接写成幂的形式:![]() (
(![]() 且
且![]() 为正整数)
为正整数)
(3)计算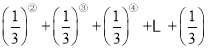
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC于D,BD=AD,DG=DC,E,F分别是BG,AC的中点.
(1)求证:DE=DF,DE⊥DF;
(2)连接EF,若AC=10,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教材中的探究:如图1,把两个边长为1的小正方形沿对角线剪开,所得的4个直角三角形拼成一个面积为2的大正方形.由此,得到了一种能在数轴上画出无理数对应点的方法.
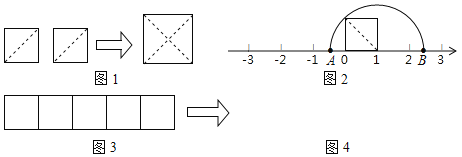
(1)图2中A、B两点表示的数分别为 , ;
(2)请你参照上面的方法,把长为5,宽为1的长方形进行裁剪,拼成一个正方形.
①在图3中画出裁剪线,并在图4位置画出所拼正方形的示意图.
②在数轴上分别标出表示数![]() 以及
以及![]() ﹣3的点,(图中标出必要线段长)
﹣3的点,(图中标出必要线段长)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面上有四个点A,B,C,D.
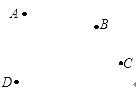
(1)根据下列语句画图:
①射线BA;
②直线AD,BC相交于点E;
③延长DC至F(虚线),使CF=BC,连接EF(虚线).
(2)图中以E为顶点的角中,小于平角的角共有__________个.
查看答案和解析>>
科目:初中数学 来源: 题型:
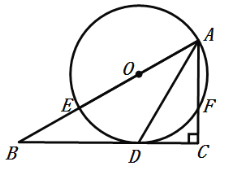
【题目】已知△ABC中∠ACB=90°,E在AB上,以AE为直径的⊙O与BC相切于D,与AC相交于F,连接AD.
(1)求证:AD平分∠BAC;
(2)连接OC,如果∠B=30°,CF=1,求OC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com