
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=AC,BC=2![]() ,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为( )
,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为( )
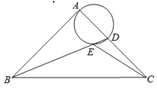
A. 3 B. 1 C. ![]() D.
D. ![]()
【答案】D
【解析】
连接AE,如图1,先根据等腰三角形的性质得到AB=AC=2,再根据圆周角定理,由AD为直径得到∠AED=90°,接着由∠AEB=90°得到点E在以AB为直径的⊙O上,于是当点O、E、C共线时,CE最小,如图2,在Rt△AOC中利用勾股定理计算出OC,从而得到CE的最小值.
连接AE,如图1,
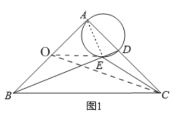
∵∠BAC=90°,AB=AC,BC=2![]() ,∴AB=AC=2,∵AD为直径,∴∠AED=90°,∴∠AEB=90°,∴点E在以AB为直径的⊙O上,∵⊙O的半径为1,连接OE,OC,∴OE=
,∴AB=AC=2,∵AD为直径,∴∠AED=90°,∴∠AEB=90°,∴点E在以AB为直径的⊙O上,∵⊙O的半径为1,连接OE,OC,∴OE=![]() AB=1,在Rt△AOC中,∵OA=2,AC=4,∴OC=
AB=1,在Rt△AOC中,∵OA=2,AC=4,∴OC=![]() =
=![]() ,由于OC=
,由于OC=![]() ,OE=1是定值,点E在线段OC上时,CE最小,如图2,
,OE=1是定值,点E在线段OC上时,CE最小,如图2,
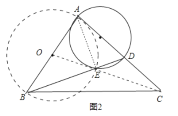
∴CE=OC-OE=![]() -1,即线段CE长度的最小值为
-1,即线段CE长度的最小值为![]() -1,故答案选D.
-1,故答案选D.


科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2+mx+m2=0.
(1)求证:不论m取何实数,该方程都有两个不相等的实数根;
(2)若该方程的一个根为1,求该方程的另一根。
查看答案和解析>>
科目:初中数学 来源: 题型:
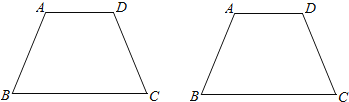
【题目】阅读下面材料,再回答问题:有一些几何图形可以被某条直线分成面积相等的两部分,我们将“把一个几何图形分成面积相等的两部分的直线叫做该图形的二分线”,如:圆的直径所在的直线是圆的“二分线”,正方形的对角线所在的直线是正方形的“二分线”。
解决下列问题:
(1)菱形的“二分线”可以是____________________________________。
(2)三角形的“二分线”可以是__________________________________。
(3)在下图中,试用两种不同的方法分别画出等腰梯形ABCD的“二分线”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数y=x2-2x-3的图象与x轴交于A,B两点,与y轴交于点C,连接BC,点D为抛物线的顶点,点P是第四象限的抛物线上的一个动点(不与点D重合).
(1)求∠OBC的度数;
(2)连接CD,BD,DP,延长DP交x轴正半轴于点E,且S△OCE=S四边形OCDB,求此时P点的坐标;
(3)过点P作PF⊥x轴交BC于点F,求线段PF长度的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中, 边AB的垂直平分线交对角线AC于点F,垂足为点E,连结DF,若∠BAD=80°,则∠CDF的度数为( )
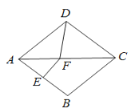
A.80°B.70°C.65°D.60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某车间的甲、乙两名工人分别同时生产![]() 只同一型号的零件,他们生产的零件
只同一型号的零件,他们生产的零件![]() (只)与生产时间
(只)与生产时间![]() (分)的函数关系的图象如图所示。根据图象提供的信息解答下列问题:
(分)的函数关系的图象如图所示。根据图象提供的信息解答下列问题:

(1)甲每分钟生产零件_______只;乙在提高生产速度之前已生产了零件_______只;
(2)若乙提高速度后,乙的生产速度是甲的![]() 倍,请分别求出甲、乙两人生产全过程中,生产的零件
倍,请分别求出甲、乙两人生产全过程中,生产的零件![]() (只)与生产时间
(只)与生产时间![]() (分)的函数关系式;
(分)的函数关系式;
(3)当两人生产零件的只数相等时,求生产的时间;并求出此时甲工人还有多少只零件没有生产.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】6月1日起,我国将全面试行居民阶梯式电价,某市出台了实施细则,具体规定如下:
设用电量为a度,当a≤150时,电价为现行电价,每度0.51元;当150<a≤240时,在现行电价基础上,每度提高0.05元;当a>240时,在现行电价基础上,每度提高0.30元.设某户的月用电量为x(度),电费为y(元).则y与x之间的函数关系的大致图像是( )
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
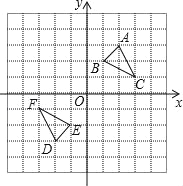
【题目】如图,△DEF是△ABC经过某种变换得到的图形,点A与点D,点B与点E,
点C与点F分别是对应点,观察点与点的坐标之间的关系,解答下列问题:
(1)分别写出点A与点D,点B与点E,点C与点F的坐标,并说说对应点的坐标有哪些特征;
(2)若点P(a+3,4﹣b)与点Q(2a,2b﹣3)也是通过上述变换得到的对应点,求a,b的值.
(3)求图中△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com