
【题目】如图,在平行四边形ABCD中,∠BAD、∠ABC的平分线AF、BG分别与线段CD交于点F、G,
AF与BG交于点E.
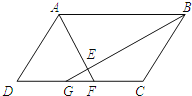
(1)求证:AF⊥BG,DF=CG;
(2)若AB=10,AD=6,AF=8,求FG和BG的长度.
【答案】(1)见解析(2)FG的长度为2,BG的长度为4![]() .
.
【解析】
试题分析:(1)由在平行四边形ABCD中,∠BAD、∠ABC的平分线AF、BG分别与线段CD交于点F、G,易求得2∠BAF+2∠ABG=180°,即可得∠AEB=90°,证得AF⊥BG,易证得△ADF与△BCG是等腰三角形,即可得AD=DF,BC=CG,又由AD=BC,即可证得DF=CG;
(2)由(1)易求得DF=CG=8,CD=AB=10,即可求得FG的长;过点B作BH∥AF交DC的延长线于点H,易证得四边形ABHF为平行四边形,即可得△HBG是直角三角形,然后利用勾股定理,即可求得BG的长.
(1)证明:∵AF平分∠BAD,
∴∠DAF=∠BAF=![]() ∠BAD.
∠BAD.
∵BG平分∠ABC,
∴∠ABG=∠CBG=![]() ∠ABC.
∠ABC.
∵四边形ABCD平行四边形,
∴AD∥BC,AB∥CD,AD=BC,
∴∠BAD+∠ABC=180°,
即2∠BAF+2∠ABG=180°,
∴∠BAF+∠ABG=90°.
∴∠AEB=180°﹣(∠BAF+∠ABG)=180°﹣90°=90°.
∴AF⊥BG;
∵AB∥CD,
∴∠BAF=∠AFD,
∴∠AFD=∠DAF,
∴DF=AD,
∵AB∥CD,
∴∠ABG=∠CGB,
∴∠CBG=∠CGB,
∴CG=BC,
∵AD=BC.
∴DF=CG;
(2)解:∵DF=AD=6,
∴CG=DF=6.
∴CG+DF=12,
∵四边形ABCD平行四边形,
∴CD=AB=10.
∴10+FG=12,
∴FG=2,
过点B作BH∥AF交DC的延长线于点H.
∴∠GBH=∠AEB=90°.
∵AF∥BH,AB∥FH,
∴四边形ABHF为平行四边形.
∴BH=AF=8,FH=AB=10.
∴GH=FG+FH=2+10=12,
∴在Rt△BHG中:BG=![]() =
=![]() .
.
∴FG的长度为2,BG的长度为4![]() .
.




 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】一次数学知识竞赛共有30道题,规定,答对一道题得4分,不答或答错一道题倒扣2分,若甲同学答对25题,答错5道题,则甲 同学得________分,若得分低于60分者获奖,则获奖者至少应答对________道题。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点M在第四象限,到x轴,y轴的距离分别为6,4,则点M的坐标为( )
A. (4,﹣6) B. (﹣4,6) C. (﹣6,4) D. (﹣6,﹣4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的一边AB为直径的半圆与其它两边AC,BC的交点分别为D、E,且=.

(1)试判断△ABC的形状,并说明理由.
(2)已知半圆的半径为5,BC=12,求sin∠ABD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个三角形的两边长分别为3 cm和7 cm,则此三角形的第三边的长可能是( )
A. 3 cm B. 4 cm C. 7 cm D. 11 cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com