
分析 (1)分解给定等式,发现“3=2×1+1,1=2×1-1,5=2×2+1,3=2×2-1,7=2×3+1,5=2×3-1”,从而得出第四个得数中该为“2×4+1=9,2×4-1=7”,在第三个等式中用9替换7,用7替换5即可得出结论;
(2)结合(1)故猜想4(2n+1)2-4(2n-1)2=32n,利用完全平方公式的展开式结合整式的加减运算法则即可证出结论成立.
解答 解:(1)观察等式4×32-4×12=32①,4×52-4×32=64②,4×72-4×52=96③,
发现3=2×1+1,1=2×1-1,5=2×2+1,3=2×2-1,7=2×3+1,5=2×3-1,
则第四个等式为:4×(2×4+1)2-4×(2×4-1)2=32×4,即4×92-4×72=128.
故答案为:4×92-4×72=128.
(2)结合(1)猜想第n个等式为:4(2n+1)2-4(2n-1)2=32n,
证明:左边=4(2n+1)2-4(2n-1)2,
=4×[4n2+4n+1-(4n2-4n+1)],
=4×8n,
=32n=右边.
故猜想成立.
点评 本题考查了规律型中的数字的变化、完全平方公式以及整式的运算,解题的关键是发现规律“4(2n+1)2-4(2n-1)2=32n”.本题属于基础题,难度不大,解决该题型题目时,根据给定等式变化找出变化规律是关键.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
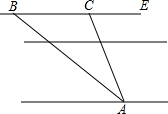 在一次测量活动中,同学们想测量某高速公路的宽度.如图,他们在该高速公路的东侧选定一广告牌A,并在西侧防护带的外沿B处观察,此时视线BA与外沿BE所成的夹角是30°,沿外沿BE向北走了8米到C处,再观察A,此时视线CA与外沿所成的夹角∠ACE=60°,已纪该高速公路西侧防护带宽1米.求此高速公路的宽约为多少米.(结果精确到1米.参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
在一次测量活动中,同学们想测量某高速公路的宽度.如图,他们在该高速公路的东侧选定一广告牌A,并在西侧防护带的外沿B处观察,此时视线BA与外沿BE所成的夹角是30°,沿外沿BE向北走了8米到C处,再观察A,此时视线CA与外沿所成的夹角∠ACE=60°,已纪该高速公路西侧防护带宽1米.求此高速公路的宽约为多少米.(结果精确到1米.参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com