
【题目】如图,把平面内一条数轴![]() 绕原点
绕原点![]() 逆时针旋转角
逆时针旋转角![]() 得到另一条数轴
得到另一条数轴![]() 轴和
轴和![]() 轴构成一个平面斜坐标系.过点
轴构成一个平面斜坐标系.过点![]() 作
作![]() 轴的平行线,交
轴的平行线,交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴的平行线,交
轴的平行线,交![]() 轴于点
轴于点![]() .若点
.若点![]() 在
在![]() 轴上对应的实数为
轴上对应的实数为![]() ,点
,点![]() 在
在![]() 轴上对应的实数为
轴上对应的实数为![]() ,则成有序实数对
,则成有序实数对![]() 为点
为点![]() 的斜坐标.
的斜坐标.
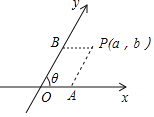
(1)在某平面斜坐标系中,已知![]() ,点
,点![]() 的斜坐标为
的斜坐标为![]() ,点
,点![]() 与点
与点![]() 关于
关于![]() 轴对称,求点
轴对称,求点![]() 的斜坐标.
的斜坐标.
(2)某平面斜坐标系中,已知点![]() ,求出点
,求出点![]() 关于
关于![]() 轴、
轴、![]() 轴的对称点
轴的对称点![]() 点、
点、![]() 点的斜坐标.(用含
点的斜坐标.(用含![]() 及
及![]() 的式子表示).
的式子表示).
(3)直接写出点![]() 关于原点对称的点的斜坐标是_________.
关于原点对称的点的斜坐标是_________.
【答案】(1) (5,-3); (2)![]() ,
,![]() ; (3)
; (3)![]()
【解析】
(1)如图,作点P关于x轴的对称点N,连接PN交x轴于F,作NC∥x轴交y轴于C,作ND∥y轴交x轴于D.求出OC,OD即可解决问题;
(2)利用(1)中的方法解决问题即可;
(3)根据斜坐标的定义写出坐标即可.
(1)如图,作点P关于x轴的对称点N,连接PN交x轴于F,作NC∥x轴交y轴于C,作ND∥y轴交x轴于D.
∵DN∥BC∥PA,
∴∠PAF=∠NDF,
∵PF=NF,∠AFP=∠NFD,
∴△AFP≌△DFN(AAS),
∴AF=DF,PA=DN=OC=b,
∵在Rt△AFP中,∠PAF=∠BOA=θ=60°,
∴AF=DF=bcos60°=![]() b,
b,
∴OD=OA+ AF+DF =![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴点N的斜坐标为(5,-3);
(2)如图,作点P关于x轴的对称点Q,连接PQ交x轴于F,作QC∥x轴交y轴于C,作QD∥y轴交x轴于D.

∵DQ∥BC∥PA,
∴∠PAF=∠QDF,
∵PF=QF,∠AFP=∠QFD,
∴△AFP≌△DFQ(AAS),
∴AF=DF,PA=DQ=OC=y,
∵在Rt△AFP中,∠PAF=∠BOA=θ,
∴AF=DF=![]() ,
,
∴DO=OA+AF+FD=![]()
∴点Q的斜坐标为![]() ,
,
如图,作点P关于y轴的对称点R,连接PR交![]() 轴于E,作RH∥
轴于E,作RH∥![]() 轴交y轴于H,作RG∥
轴交y轴于H,作RG∥![]() 轴交
轴交![]() 轴于G.
轴于G.

同理可证得△EBP≌△EHR(AAS),
∴BE=EH,PB=RH=OA=![]() ,
,
∵在Rt△EBP中,∠EBP=∠BOA=θ,
∴BE=EH =![]() cos
cos![]() ,
,
∴HO=OB+BE+EH=![]() ,
,
∴点R的坐标为![]() ;
;
(3)如图,点P关于原点的对称点![]() ,作
,作![]() ∥
∥![]() 轴交
轴交![]() 轴于M.
轴于M.

∵![]() ∥PB∥OA,
∥PB∥OA,![]()
∴△![]() ≌△PBO,
≌△PBO,
∴![]() ,
,![]() ,
,
∴![]() 关于原点对称的点的斜坐标是
关于原点对称的点的斜坐标是![]() ,
,
故答案为:![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】小明正在做一个半径为![]() 米的地球模型.
米的地球模型.
(1)他想用一根铁丝围住地球模型的赤道,大约需要多少的铁丝?如果要把这个模型的半径增加![]() 米,要围住赤道需要增加多长的铁丝?
米,要围住赤道需要增加多长的铁丝?
(2)假设真的为地球赤道做一个铁箍,大约要多长的铁丝?如果将铁箍所围的半径增加![]() 米,那么需要增加多长的铁丝?(地球半径约为
米,那么需要增加多长的铁丝?(地球半径约为![]() 千米)
千米)
(3)比较(1)(2)的结果,请叙述一下你发现了什么?
(4)如果小明做的地球的模型的半径为![]() ,如果地球体积是地球模型体积的
,如果地球体积是地球模型体积的![]() 倍,求
倍,求![]() 的值.(球的体积公式
的值.(球的体积公式![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某公园里一处矩形风景欣赏区ABCD,长AB=50米,宽BC=25米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为1米,那小明沿着小路的中间,从出口A到出口B所走的路线(图中虚线)长为___________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,菱形
中,菱形![]() 的顶点
的顶点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在第一象限内,对角线
在第一象限内,对角线![]() 与
与![]() 轴平行,直线
轴平行,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() .将菱形
.将菱形![]() 沿
沿![]() 轴向左平移
轴向左平移![]() 个单位.当点
个单位.当点![]() 落在
落在![]() 的内部时(不包括三角形的边),则
的内部时(不包括三角形的边),则![]() 的取值范围是__________.
的取值范围是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线![]() 的解析式为
的解析式为![]() ,分别交
,分别交![]() 轴、
轴、![]() 轴于点
轴于点![]() .
.

(1)写出![]() 两点的坐标,并画出直线
两点的坐标,并画出直线![]() 的图象.(不需列表);
的图象.(不需列表);
(2)将直线![]() 向左平移4个单位得到
向左平移4个单位得到![]() 交
交![]() 轴于点
轴于点![]() .作出
.作出![]() 的图象,
的图象,![]() 的解析式是___________.
的解析式是___________.
(3)过![]() 的顶点能否画出直线把
的顶点能否画出直线把![]() 分成面积相等的两部分?若能,可以画出几条?直接写出满足条件的直线解析式.(不必在图中画出直线)
分成面积相等的两部分?若能,可以画出几条?直接写出满足条件的直线解析式.(不必在图中画出直线)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】位于张家界核心景区的贺龙铜像,是我国近百年来最大的铜像.铜像由像体AD和底座CD两部分组成.如图,在Rt△ABC中,∠ABC=70.5°,在Rt△DBC中,∠DBC=45°,且CD=2.3米,求像体AD的高度(最后结果精确到0.1米,参考数据:sin70.5°≈0.943,cos70.5°≈0.334,tan70.5°≈2.824)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿直线DE折叠后,使得点B与点A重合.已知AC=5cm,△ADC的周长为17cm,则BC的长为( )
A.7cm
B.10cm
C.12cm
D.22cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC外切于⊙O,切点分别为点D,E,F,∠A=60°,BC=7,⊙O的半径为![]() .求:(1)求BF+CE的值; (2)求△ABC的周长.
.求:(1)求BF+CE的值; (2)求△ABC的周长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com