
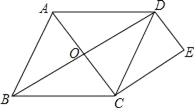
【题目】如图,在菱形ABCD中,对角线AC,BD相交于点O,过点C作CE∥BD,过点D作DE∥AC,CE与DE相交于点E.
(1)求证:四边形CODE是矩形;
(2)若AB=10,AC=12,求四边形CODE的周长.
【答案】(1)证明见解析(2)28
【解析】
(1)如图,首先证明四边形CODE是平行四边形,然后证明∠DOC=90°,即可解决问题.(2)如图,首先证明CO=AO=6, ∠AOB=90°;运用勾股定理求出BO,即可解决问题.
(1)∵CE∥BD,DE∥AC,
∴四边形CODE是平行四边形,
∵四边形ABCD是菱形
∴∠DOC=90°,
∴四边形CODE是矩形;
(2)∵四边形ABCD为菱形,
∴AO=OC=![]() AC=6,OD=OB,∠AOB=90°,
AC=6,OD=OB,∠AOB=90°,
由勾股定理得:
BO2=AB2﹣AO2,而AB=10,
∴DO=BO=![]() =8,
=8,
由(1)得四边形CODE是矩形,
∴四边形CODE的周长=2(6+8)=28.


科目:初中数学 来源: 题型:
【题目】如图1,一等腰直角三角尺GEF的两条直角边与正方形ABCD的两条边分别重合在一起.现正方形ABCD保持不动,将三角尺GEF绕斜边EF的中点O(点O也是BD中点)按顺时针方向旋转.
(1)如图2,当EF与AB相交于点M,GF与BD相交于点N时,通过观察或测量BM,FN的长度,猜想BM,FN满足的数量关系,并证明你的猜想;
(2)若三角尺GEF旋转到如图3所示的位置时,线段FE的延长线与AB的延长线相交于点M,线段BD的延长线与GF的延长线相交于点N,此时,(1)中的猜想还成立吗?若成立,请证明;若不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应党中央“下好一盘棋,共护一江水”的号召,某治污公司决定购买甲、乙两种型号的污水处理设备共10台.经调查发现:购买一台甲型设备比购买一台乙型设备多2万元,购买2台甲型设备比购买3台乙型设备少6万元,且一台甲型设备每月可处理污水240吨,一台乙型设备每月可处理污水200吨.
(1)请你计算每台甲型设备和每台乙型设备的价格各是多少万元?
(2)若治污公司购买污水处理设备的资金不超过109万元,月处理污水量不低于2080吨.
①求该治污公司有几种购买方案;
②如果为了节约资金,请为该公司设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,顶点为(4,1)的抛物线交y轴于点A,交x轴于B,C两点(点B在点C的左侧),已知C点坐标为(6,0).
(1)求此抛物线的解析式;
(2)连结AB,过点B作线段AB的垂线交抛物线于点D,如果以点C为圆心的圆与抛物线的对称轴l相切,先补全图形,再判断直线BD与⊙C的位置关系并加以证明;
(3)已知点P是抛物线上的一个动点,且位于A,C两点之间.问:当点P运动到什么位置时,△PAC的面积最大?求出△PAC的最大面积.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图中,AE⊥AB且AE=AB,BC⊥CD且BC=CD,若点E、B、D到直线AC的距离分别为6、3、2,则图中实线所围成的阴影部分面积S是( )

A.50B.44C.38D.32
查看答案和解析>>
科目:初中数学 来源: 题型:
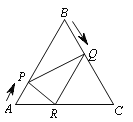
【题目】如图,已知△ABC是边长为6cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC匀速运动,其中点P运动的速度是1cm/s,点Q运动的速度是2cm/s,当点Q到达点C时,P、Q两点都停止运动,设运动时间为t(s),解答下列问题:
(1)当t=2时,判断△BPQ的形状,并说明理由;
(2)设△BPQ的面积为S(cm2),求S与t的函数关系式;
(3)作QR//BA交AC于点R,连结PR,当t为何值时,△APR∽△PRQ?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC=6cm,BC=4cm,点D为AB的中点.
⑴如果点P在线段BC上以1cm/s的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动.
①若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CPQ是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为______cm/s时,在某一时刻也能够使△BPD与△CPQ全等.
⑵若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都按逆时针方向沿△ABC的三边运动.求经过多少秒后,点P与点Q第一次相遇,并写出第一次相遇点在△ABC的哪条边上?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,∠A=140°,∠D=80°.

(1)如图1,若∠B=∠C,试求出∠C的度数;
(2)如图2,若∠ABC的角平分线BE交DC于点E,且BE∥AD,试求出∠C的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
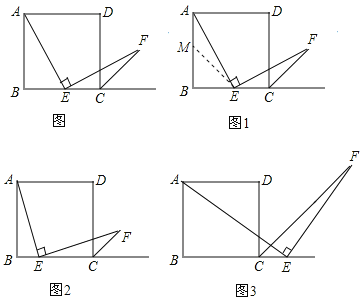
【题目】如图,四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形外角平分线CF于点F.请你认真阅读下面关于这个图的探究片段,完成所提出的问题.
(1)探究1:小强看到图(*)后,很快发现AE=EF,这需要证明AE和EF所在的两个三角形全等,但△ABE和△ECF显然不全等(一个是直角三角形,一个是钝角三角形),考虑到点E是边BC的中点,因此可以选取AB的中点M,连接EM后尝试着去证△AEM≌EFC就行了,随即小强写出了如下的证明过程:
证明:如图1,取AB的中点M,连接EM.
∵∠AEF=90°
∴∠FEC+∠AEB=90°
又∵∠EAM+∠AEB=90°
∴∠EAM=∠FEC
∵点E,M分别为正方形的边BC和AB的中点
∴AM=EC
又可知△BME是等腰直角三角形
∴∠AME=135°
又∵CF是正方形外角的平分线
∴∠ECF=135°
∴△AEM≌△EFC(ASA)
∴AE=EF
(2)探究2:小强继续探索,如图2,若把条件“点E是边BC的中点”改为“点E是边BC上的任意一点”,其余条件不变,发现AE=EF仍然成立,请你证明这一结论.
(3)探究3:小强进一步还想试试,如图3,若把条件“点E是边BC的中点”改为“点E是边BC延长线上的一点”,其余条件仍不变,那么结论AE=EF是否成立呢?若成立请你完成证明过程给小强看,若不成立请你说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com