
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,P是△ABC形内一点,且∠APB=∠APC=135°.
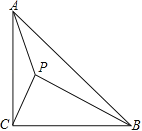
(1)求证:△CPA∽△APB;
(2)试求tan∠PCB的值.
【答案】(1)见解析 (2)2.
【解析】
试题(1)根据∠PBA+∠PAB=45°和∠PAC+∠PAB=45°得出∠PAC=∠PBA,再根据已知条件∠APB=∠APC得出三角形相似;(2)根据等腰直角三角形的性质得出CA和AB的比值,设CP=k,则PB=2k,然后根据∠BPC=90°求出∠PCB的正切值.
试题解析:(1)∵在△ABC中,∠ACB=90°,AC=BC,∴∠BAC=45°,即∠PAC+∠PAB=45°,
又在△APB中,∠APB=135°, ∴∠PBA+∠PAB=45°, ∴∠PAC=∠PBA,
又∠APB=∠APC, ∴△CPA∽△APB.
(2)∵△ABC是等腰直角三角形,
∴![]() , 又∵△CPA∽△APB, ∴
, 又∵△CPA∽△APB, ∴![]() ,
,
令CP=k,则![]() ,
,
又在△BCP中,∠BPC=360°﹣∠APC﹣∠APB=90°, ∴![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,某一时刻,小宁站在斜坡AC上的A处,小李在大楼FD的楼顶F处,此时小宁望小李的仰角为18.43°.5秒后,小宁沿斜坡AC前进到达C处,小李从大楼F处下楼到大楼E处,此时小李望小宁的俯角为22.6°;然后小李继续下楼,小宁沿CD前往楼底D处,已知小宁的速度为5.2米/秒,大楼FD的高度为30米,斜坡AC的坡度为1:2.4,小李、小宁都保持匀速前进,若斜坡、大楼在同一平面内,小李、小宁的身高忽略不计,则当小李达到楼底D处时,小宁距离D处的距离为( )米.
(已知:tan18.43°≈![]() ,sin18.43°≈
,sin18.43°≈![]() ,cos22.6°≈
,cos22.6°≈![]() ,tan22.6≈
,tan22.6≈![]() )
)

A.10B.15.6C.20.4D.26
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】文具店有三种品牌的6个笔记本,价格是4,5,7(单位:元)三种,从中随机拿出一个本,已知![]() (一次拿到7元本)
(一次拿到7元本)![]() .
.
(1)求这6个本价格的众数.
(2)若琪琪已拿走一个7元本,嘉嘉准备从剩余5个本中随机拿一个本.
①所剩的5个本价格的中位数与原来6个本价格的中位数是否相同?并简要说明理由;
②嘉嘉先随机拿出一个本后不放回,之后又随机从剩余的本中拿一个本,用列表法求嘉嘉两次都拿到7元本的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知抛物线![]() 经过点A(0,3),B(3,0),C(4,3).
经过点A(0,3),B(3,0),C(4,3).
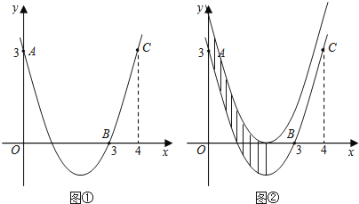
(1)求抛物线的函数表达式;
(2)求抛物线的顶点坐标和对称轴;
(3)把抛物线向上平移,使得顶点落在x轴上,直接写出两条抛物线、对称轴和y轴围成的图形的面积S(图②中阴影部分).
查看答案和解析>>
科目:初中数学 来源: 题型:
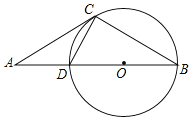
【题目】如图,点A是⊙O直径BD延长线上的一点,AC是⊙O的切线,C为切点.AD=CD,
(1)求证:AC=BC;
(2)若⊙O的半径为1,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为引导学生广泛阅读文学名著,某校在七年级、八年级开展了读书知识竞赛,该校七、八年级各有学生![]() 人,各随机抽取
人,各随机抽取![]() 名学生进行了抽样调查,获得了他们知识竞赛成绩(分),并对数据进行整理、描述和分析.下面给出了部分信息.
名学生进行了抽样调查,获得了他们知识竞赛成绩(分),并对数据进行整理、描述和分析.下面给出了部分信息.
七年级:
![]()
八年级:
![]()
成绩人数 |
|
|
|
|
|
七年级 |
|
|
|
|
|
八年级 |
|
|
|
|
|
平均数、中位数、众数如表所示:
年级 | 平均数 | 中位数 | 众数 |
七年级 |
|
|
|
八年级 |
|
|
|
根据以上信息,回答下列问题:
![]()
![]() ,
,![]() ,
,![]() _
_
![]() 该校对读书知识竞赛成绩不少于
该校对读书知识竞赛成绩不少于![]() 分的学生授予“阅读小能手”称号,请你估计该校七、八年级所有学生中获得“阅读小能手”称号的大约有 人;
分的学生授予“阅读小能手”称号,请你估计该校七、八年级所有学生中获得“阅读小能手”称号的大约有 人;
![]() 结合以数据,你认为哪个年级读书知识竞赛的总体成绩较好,说明理由
结合以数据,你认为哪个年级读书知识竞赛的总体成绩较好,说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰三角形ABC中,∠BAC=90°,AB=AC=2,D是BC边上的一个动点,(不与B、C重合)在AC边上取一点E,使∠ADE=45°.
(1)求证:△ABD∽△DCE;
(2)设BD=x,AE=y.
①求y关于x的函数关系式并写出自变量x的取值范围;
②求y的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工艺品店购进A,B两种工艺品,已知这两种工艺品的单价之和为200元,购进2个A种工艺品和3个B种工艺品需花费520元.
(1)求A,B两种工艺品的单价;
(2)该店主欲用9600元用于进货,且最多购进A种工艺品36个,B种工艺品的数量不超过A种工艺品的2倍,则共有几种进货方案?
(3)已知售出一个A种工艺品可获利10元,售出一个B种工艺品可获利18元,该店主决定每售出一个B种工艺品,为希望工程捐款m元,在(2)的条件下,若A,B两种工艺品全部售出后所有方案获利均相同,则m的值是多少?此时店主可获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
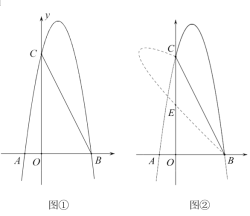
【题目】如图①,抛物线![]() 过
过![]() 、
、![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,连接
,连接![]() .
.
(1)求该抛物线的表达式和对称轴;
(2)点![]() 是抛物线对称轴上一动点,当
是抛物线对称轴上一动点,当![]() 是以
是以![]() 为直角边的直角三角形时,求所有符合条件的点
为直角边的直角三角形时,求所有符合条件的点![]() 的坐标;
的坐标;
(3)如图②,将抛物线在![]() 上方的图象沿
上方的图象沿![]() 折叠后与
折叠后与![]() 轴交与点
轴交与点![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com