
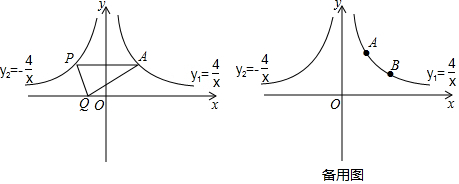
分析 (1)先求出点A的坐标,进而得出点P的坐标,最后用三角形的面积公式即可得出结论;
(2)分三种情况,利用等腰直角三角形和AP∥x轴建立方程求解即可;
(3)利用等腰三角形的两腰相等建立方程即可得出结论.
解答 解:(1)∵点A、B是函数y1=$\frac{4}{x}$(x>0)图象上的两点,
∴A(m,$\frac{4}{m}$),B(n,$\frac{4}{n}$),
∵AP∥x轴,
∴点P的纵坐标为$\frac{4}{m}$,
∵点P是y2=-$\frac{4}{x}$(x<0)的图象上的一点,
∴x=-m,
∴P(-m,$\frac{4}{m}$),
∴AP=2m,
∴S△APQ=$\frac{1}{2}$AP•yA=$\frac{1}{2}$•2m•$\frac{4}{m}$=4;
(2)∵△APQ是等腰直角三角形,
∴①当∠APQ=90°时,
∴PQ⊥x轴,
∴PQ=$\frac{4}{m}$,
∵AP=2m,
∵AP=PQ,
∴2m=$\frac{4}{m}$,
∴m=-$\sqrt{2}$(舍)或m=$\sqrt{2}$,
∴P(-$\sqrt{2}$,2$\sqrt{2}$),
∴Q(-$\sqrt{2}$,0),
②当∠PAQ=90°,
∴AQ⊥x轴,
∴AQ=$\frac{4}{m}$,
∵AP=2m,
∵AP=PQ,
∴2m=$\frac{4}{m}$,
∴m=-$\sqrt{2}$(舍)或m=$\sqrt{2}$,
∴A($\sqrt{2}$,2$\sqrt{2}$),
∴Q($\sqrt{2}$,0),
③当∠AQP=90°时,AQ=PQ,
∵AP∥x轴,
∴点Q是AP的垂直平分线上,
∵函数y1与y2关于y轴对称,
∴点Q(0,0),此时,$\frac{4}{m}$=m,即m=-2(舍)或m=2,
综上所述,满足条件的点Q为(-$\sqrt{2}$,0),(0,0),($\sqrt{2}$,0);
(3)∵A(m,$\frac{4}{m}$),B(n,$\frac{4}{n}$),
∴OA2=m2+($\frac{4}{m}$)2,OB2=n2+($\frac{4}{n}$)2,
∵△OAB是以AB为底的等腰三角形,
∴OA=OB,
∴OA2=OB2,
∴m2+($\frac{4}{m}$)2=n2+($\frac{4}{n}$)2,
∴m2-n2=($\frac{4}{n}$)2-($\frac{4}{m}$)2,
∴(m+n)(m-n)=($\frac{4}{n}$+$\frac{4}{m}$)($\frac{4}{n}$-$\frac{4}{m}$)=$\frac{4}{mn}$(m+n)•$\frac{4}{mn}$(m-n),
∵m≠n,
∴(mn)2=16,
∴mn=-4(舍)或mn=4,
即:mn=4.
点评 此题是反比例函数综合题,主要考查了反比例函数的性质,等腰直角三角形的性质,等腰三角形的性质,解(1)的关键是表示出AP,解(2)的关键是分类讨论,解(3)的关键是利用等腰三角形的两腰建立方程求解,是一道中等难度的中考常考题.


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 在5×5的正方形网格中,每个小正方形的边长为1,用四边形覆盖如图所示,被覆盖的网格线中,竖直部分的线段的长度之和记作m,水平部分的线段的长度之和记作n,则m-n=( )
在5×5的正方形网格中,每个小正方形的边长为1,用四边形覆盖如图所示,被覆盖的网格线中,竖直部分的线段的长度之和记作m,水平部分的线段的长度之和记作n,则m-n=( )| A. | 0 | B. | 0.5 | C. | -0.5 | D. | 0.75 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,正方形ABCD的四个顶点A、B、C、D正好分别在四条平行线l1、l3、l4、l2上.若从上到下每两条平行线间的距离都是2cm,则正方形ABCD的面积为20cm2.
如图,正方形ABCD的四个顶点A、B、C、D正好分别在四条平行线l1、l3、l4、l2上.若从上到下每两条平行线间的距离都是2cm,则正方形ABCD的面积为20cm2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
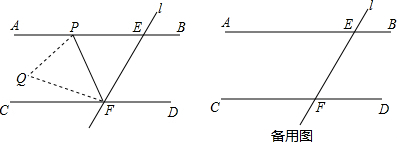
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com