解:(1)证明:∵CO=CD,∠OCD=60°,
∴△COD是等边三角形;
(2)解:当∠BOC=150°时,△AOD是直角三角形.
∵△BCO绕C顺时针方向旋转60°得到△ADC,
∴△BOC≌△ADC,
∴∠ADC=∠BOC=150°,OB=AD,
又∵△COD是等边三角形,
∴∠ODC=60°,OC=OD
∴∠ADO=90°,
即△AOD是直角三角形;
∴OA
2=OD
2+AD
2,
∴OA
2=OC
2+AO
2;
解题目1:
解:将△BCO绕C顺时针方向旋转90°得到△ADC,连接OD,如图,
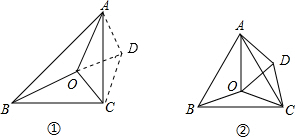
∴△BOC≌△ADC,
∴OC=CD=1,OB=AD=

,
∵∠OCD=90°且OC=CD=1,
∴∠COD=45°,OD=

.
又∵OA=

,
∴AD
2=OA
2+OD
2
∴∠AOD=90°
∴∠AOC=∠COD+∠AOD=135°.
分析:题目2:(1)根据有一个角为60°的等腰三角形是等边三角形直接进行判定即可;
(2)根据旋转的性质,得到△BOC≌△ADC,从而求出∠ADC的度数,OB=AD,再根据等边三角形的性质得∠ODC=60°,OC=OD,即∠ADO=90°,即可以判断△AOD的形状,及OA、OB、OC三者之间的等量关系式.
题目1:根据题目2的方法,将△BCO绕C顺时针方向旋转90°得到△ADC,连接OD,可得到△BOC≌△ADC,即∠OC=CD=1,OB=AD=

,再利用等腰直角三角形的性质得出∠COD的度数;
最后利用勾股定理的逆定理证明△AOD是直角三角形,易得∠AOC的度数.
点评:本题考查了旋转的性质,等边三角形的判定和性质,直角三角形的性质等知识.注意此题有一定的开放性,要找到变化中的不变量才能有效解决问题.

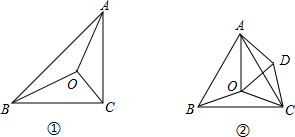 星期天,小明在解答下列题目时卡壳了.
星期天,小明在解答下列题目时卡壳了. ,OB=
,OB= .求∠AOC的度数.
.求∠AOC的度数.
 ,
, .
. ,
, ,再利用等腰直角三角形的性质得出∠COD的度数;
,再利用等腰直角三角形的性质得出∠COD的度数;

 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案 (2011•清流县质检)星期天,小明在解答下列题目时卡壳了.
(2011•清流县质检)星期天,小明在解答下列题目时卡壳了. (2012•益阳)已知:如图,抛物线y=a(x-1)2+c与x轴交于点A(1-
(2012•益阳)已知:如图,抛物线y=a(x-1)2+c与x轴交于点A(1- (2013•宁化县质检)已知:如图,抛物线y=ax2+bx+c与x轴交于点A(1-
(2013•宁化县质检)已知:如图,抛物线y=ax2+bx+c与x轴交于点A(1-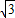 ,OB=
,OB= .求∠AOC的度数.
.求∠AOC的度数.